オペアンプを用いたコンパレータ動作時におけるヒステリシス回路の考え方

はじめに

こんにちは。こんばんは。おはようございます。おやすみなさい。第2種電気工事士に受かった電気エンジニアのyokoyamaです。

今回はオペアンプを使ったコンパレータ動作にヒステリシス回路を追加し、その動作原理についての説明と数種回路について閾値計算のアプローチ手法を説明したいと思います。

コンパレータとは、簡単にいうと電気の大小判定する部品です。
とはいっても、実際に使うにあたってヒステリシスの設定をしなければならない場面が多く、意外と使い方が難しい部品でもあります。また、オープンコレクタ出力のものが多く、単純なオペアンプの理論が適用できない場面も多々あります。そういった場面ごとによる解説をしていきます。

動作原理

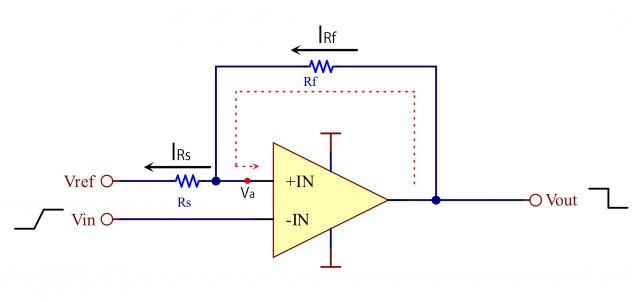
オペアンプの+端子にフィードバックを行うと、コンパレータ動作にヒステリシスをつけることができます。

この回路(反転コンパレータ)の動作はVa(=+端子)の電圧を跨いだ時に出力信号がパルス状に変化しますが、+端子にフィードバックが施されている為、Vaの電圧が下記のとおり、出力信号の影響を受けます。

\begin{align*} &\LARGE I_{Rf}=\frac{V_{out}-V_a}{R_f}\\[5mm] &\LARGE I_{Rs}=\frac{V_a-V_{ref}}{R_s}\\[5mm] &\LARGE I_{Rs}=I_{Rs}　\largeより\\[5mm] &\LARGE \frac{V_{out}-V_a}{R_f}=\frac{V_a-V_{ref}}{V_s}\\[5mm] &\LARGE ∴V_a=\frac{R_fV_{ref}+R_sV_{out}}{R_f+R_s} \end{align*}

たとえば、入力信号がLowのときは、出力信号VoutはHiの為、上記式の分子が大きくなり、Va電圧もその分上昇します。

反対に、入力信号がHiのときは、出力信号VoutはLowの為、上記式の分子が小さくなり、Va電圧もその分下降します。

グラフにあらわすと、下図のような特性(ヒステリシス特性)となるわけです。

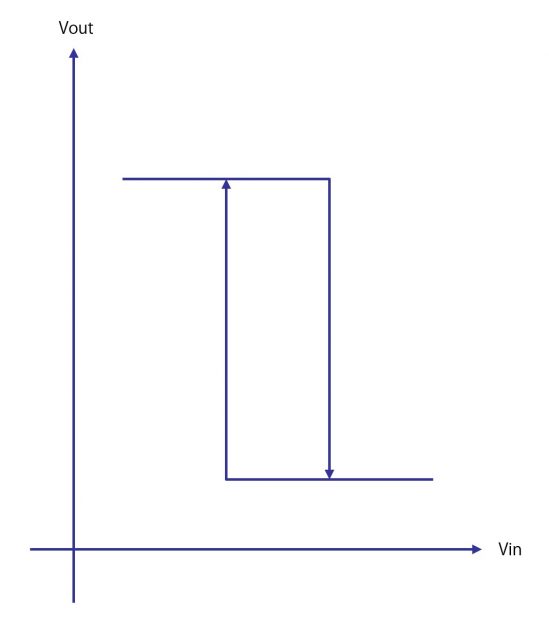
閾値計算

基本

ヒステリシス付きコンパレータの閾値はVa電圧を求めることで知ることができます。

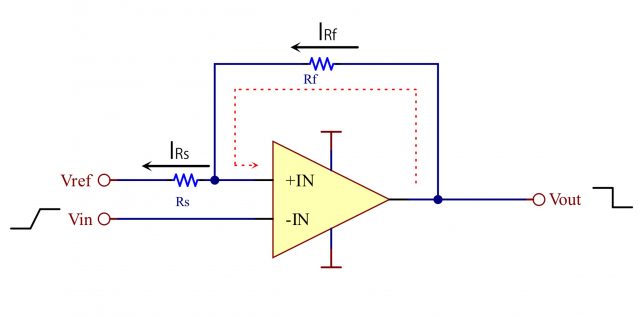
コンパレータの閾値は、Va(=+端子)電圧ですので、下記計算式より、求めることができます。

\LARGE V_a=\frac{R_fV_{ref}+R_sV_{out}}{R_f+R_s}

入力信号がLow→Hiに変化する場合

上記回路の場合、入力信号がLow→Hiに変化する場合の閾値は、変化前のVoutは(+)側飽和電圧のVpであるので、

\LARGE V_a=\frac{R_fV_{ref}+R_sV_p}{R_f+R_s}

入力信号がHi→Lowに変化する場合

入力信号がHi→Lowに変化する場合の閾値は、変化前のVoutは(-)側飽和電圧のVnであるので、

\LARGE V_a=\frac{R_fV_{ref}+R_sV_n}{R_f+R_s}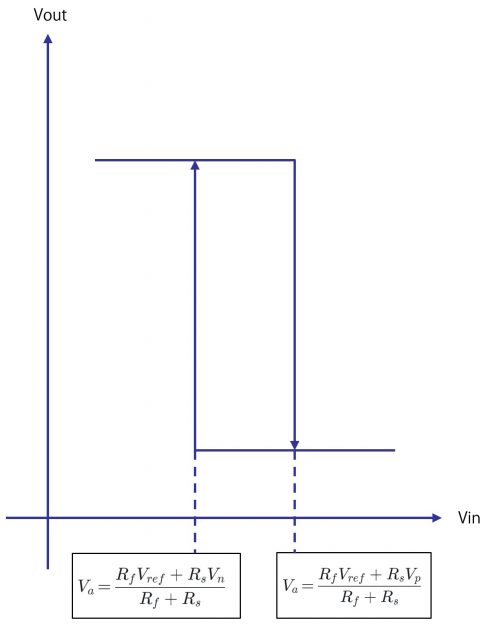

オープンコレクタ

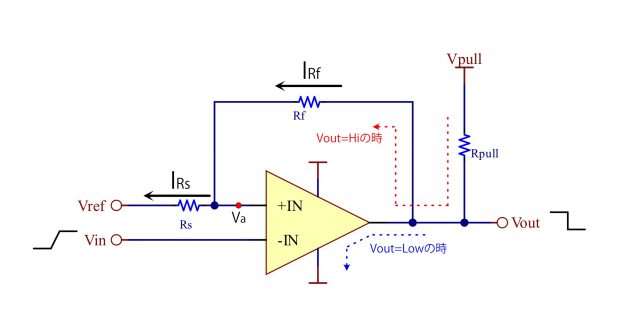
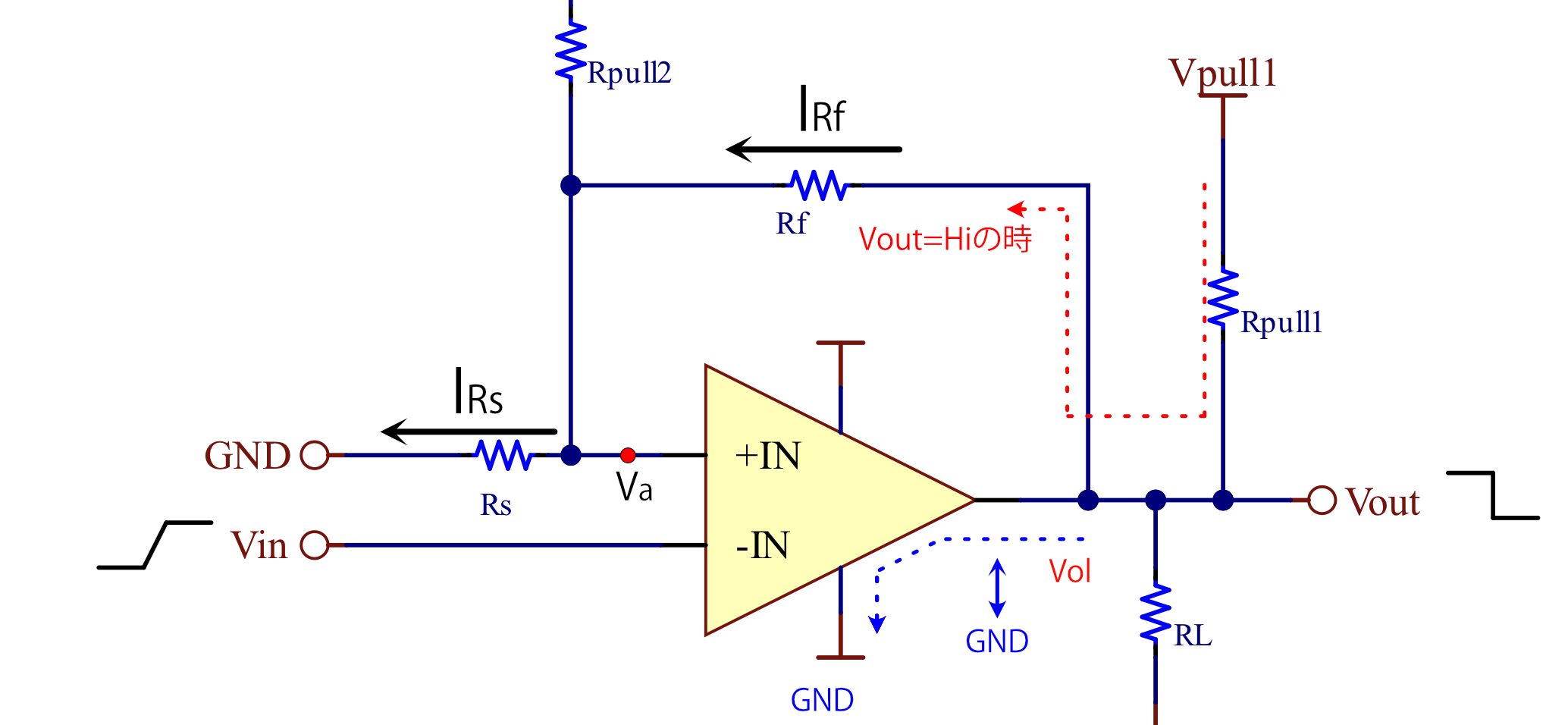
オープンコレクタのコンパレータは、Voutの出力状態により、電流ルートが異なるため、閾値の計算が変わってきますので注意が必要です。

入力信号がLow→Hiに変化する場合

上記回路の場合、入力信号がLow→Hiに変化する場合の閾値は、回路電流が赤い矢印のルートを通るため、VpullとRpullの影響を受けます。

\LARGE V_a=\frac{(R_f+R_{pull})V_{ref}+R_sV_{pull}}{(R_f+R_{pull})+R_s}

入力信号がHi→Lowに変化する場合

入力信号がHi→Lowに変化する場合の閾値は、回路電流が青い矢印のルート(通常のオペアンプと同じ)を通るため、計算式は変わりません。

\LARGE V_a=\frac{R_fV_{ref}+R_sV_n}{R_f+R_s}

Vout=Hiの場合

一方、Voutは、出力がHiの場合、Rf＋RsとRpullの分圧となるため、下記の計算式となります。(Low側はVout=Vnとなります)

\begin{align*} &\LARGE I_{Rpull}=\frac{V_{pull}-V_{out}}{R_{pull}}\\[7mm] &\LARGE I_{R}=\frac{V_{out}-V_{ref}}{R_f+R_s}\\[7mm] &\LARGE \frac{V_{pull}-V_{out}}{R_{pull}}=\frac{V_{out}-V_{ref}}{R_f+R_s}\\[7mm] &\LARGE V_{out}=\frac{(R_f+R_s)V_{pull}+R_{pull}V_{ref}}{R_{pull}+R_f+R_s}\\[7mm] &\LARGE ∴V_{out}(Hi)=V_{pull}-\frac{R_{pull}(V_{ref}-V_{pull})}{R_{pull}+R_f+R_s} \end{align*}

オープンコレクタ(2)

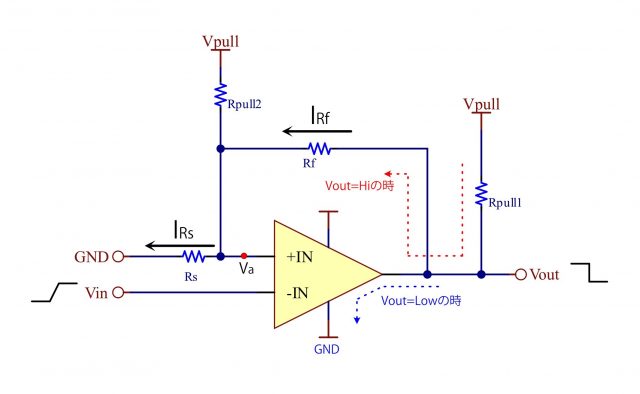
Vaに中点電位を持たせたい等の理由で、上図の様な回路を組む場合がありますが、検証してみましょう。

入力信号がLow→Hiに変化する場合

入力信号がLow→Hiに変化する場合の閾値は、上記回路の場合、

\begin{align*} &\LARGE I_{Rpull1}=I_{Rf}=\frac{V_{pull}-V_a}{R_{pull1}+R_f}\\[3mm] &\LARGE I_{Rs}=\frac{V_a}{R_s}\\[3mm] &\LARGE I_{Rpull2}=\frac{V_{pull}-V_a}{R_{pull2}}\\[8mm] &\LARGE I_{Rf}+I_{Rpull2}=I_{Rs}　\largeより、\\[3mm] &\LARGE \frac{V_{pull}-V_a}{R_{pull1}+R_f}+\frac{V_{pull}-V_a}{R_{pull2}}=\frac{V_a}{R_s} \end{align*}

従って、Low→Hiの閾値は以下となります。

\begin{align*} &\LARGE V_a=V_{pull}\cfrac{ \cfrac{1}{R_{pull1}+R_f}+\cfrac{1}{R_{pull2}} }{\cfrac{1}{R_s}+\cfrac{1}{R_{pull2}}+\cfrac{1}{R_{pull1}+R_f}} \end{align*}

入力信号がHi→Lowに変化する場合

入力信号がHi→Lowに変化する場合の閾値は、上記回路の場合は、Vout=GNDとすると、回路にVpull1の影響がありません。

\begin{align*} &\LARGE I_{Rf}=\frac{V_{out}-V_a}{R_f}\\[3mm] &\LARGE I_{Rs}=\frac{V_a}{R_s}\\[5mm] &\LARGE I_{Rpull2}=\frac{V_{pull}-V_a}{R_{pull2}}\\[8mm] &\LARGE I_{Rf}+I_{Rpull2}=I_{Rs}　\largeより、\\[5mm] &\LARGE \frac{V_{out}-V_a}{R_f}+\frac{V_{pull}-V_a}{R_{pull2}}=\frac{V_a}{R_s}\\[8mm] &\LARGE V_a=\cfrac{ \cfrac{V_{out}}{R_f}+\cfrac{V_{pull}}{R_{pull2}} }{\cfrac{1}{R_{pull2}}+\cfrac{1}{R_f}+\cfrac{1}{R_s}}\\[18mm] \end{align*}

Vout=0としない場合は、この式を使用します。
ここで、VoutはGNDで飽和しているとすると、Vout=0

従って、Hi→Lowの閾値は、以下のようになります。

\LARGE V_a=V_{pull}\cfrac{ \cfrac{R_fR_s}{R_f+R_s} }{R_{pull2}+\cfrac{R_fR_s}{R_f+R_s}}

Vout=Hiの場合

Voutは、出力がHiの場合、下記の計算式となります。
(Low側はVout=GNDとします)

\begin{align*} &\LARGE I_{Rf}=\frac{V_{out}-V_a}{R_f}\\[3mm] &\LARGE I_{Rpull1}=\frac{V_{pull}-V_{out}}{R_{pull1}}\\[5mm] &\LARGE I_{Rs}=\frac{V_a}{R_s}\\[3mm] &\LARGE I_{Rpull2}=\frac{V_{pull}-V_a}{R_{pull2}}\\[5mm] &\LARGE I_{Rf}=I_{Rpull1}　・・・(1)\\[3mm] &\LARGE I_{Rf}+I_{Rpull2}=I_{Rs}　・・・(2)\\[8mm] \end{align*}

(1)より

\begin{align*} &\LARGE \frac{V_{out}-V_a}{R_f}=\frac{V_{pull}-V_{out}}{R_{pull1}}\\[8mm] &\LARGE V_a=V_{out}-(V_{pull}-V_{out})\frac{R_f}{R_{pull1}}\\[8mm] &\LARGE V_a=\frac{V_{out}(R_{pull1}+R_f)-V_{pull}R_f}{R_{pull1}}　・・・(3)\\[8mm] \end{align*}

(2)より

\begin{align*} &\LARGE \frac{V_{out}-V_a}{R_f}+\frac{V_{pull}-V_a}{R_{pull2}}=\frac{V_a}{R_s}\\[3mm] &\LARGE \frac{V_{out}}{R_f}+\frac{V_{pull}}{R_{pull2}}=V_a\Biggl({\cfrac{1}{R_{pull2}}+\cfrac{1}{R_f}+\cfrac{1}{R_s}}\Biggl)\\[10mm] \end{align*}

(3)を代入して、

\begin{align*} &\LARGE\frac{V_{out}}{R_f}+\frac{V_{pull}}{R_{pull2}}\\[8mm] &\LARGE=\frac{V_{out}(R_{pull1}+R_f)-V_{pull}R_f}{R_{pull1}}\Biggl({\cfrac{1}{R_{pull2}}+\cfrac{1}{R_f}+\cfrac{1}{R_s}}\Biggl)\\[10mm] \end{align*}

従って、出力電圧は以下となります。

\begin{align*} &\LARGE V_{out}=\cfrac{ \cfrac{V_{pull}R_f}{R_{pull1}}\Biggl({\cfrac{1}{R_{pull2}}+\cfrac{1}{R_f}+\cfrac{1}{R_s}}\Biggl)+\cfrac{V_{pull}}{R_{pull2}}}{\cfrac{R_{pull1}+R_f}{R_{pull1}}\Biggl({\cfrac{1}{R_{pull2}}+\cfrac{1}{R_f}+\cfrac{1}{R_s}}\Biggl)-\cfrac{1}{R_f}}\\[20mm] \end{align*}

オープンコレクタ(3)

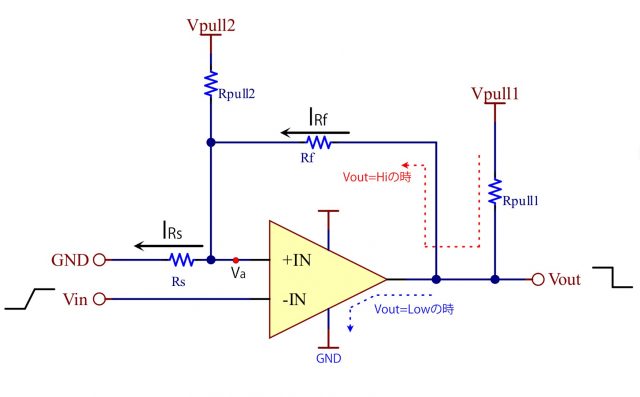
Vaに中点電位を持たせたい等の理由で、下記の様な回路を組む場合がありますが、検証してみましょう。
(2)回路との違いは、プルアップ電圧がVpull1,Vpull2に分かれている点です。

入力信号がLow→Hiに変化する場合

入力信号がLow→Hiに変化する場合の閾値は、上記回路の場合、

\begin{align*} &\LARGE I_{Rpull1}=I_{Rf}=\frac{V_{pull1}-V_a}{R_{pull1}+R_f}\\[3mm] &\LARGE I_{Rs}=\frac{V_a}{R_s}\\[6mm] &\LARGE I_{Rpull2}=\frac{V_{pull2}-V_a}{R_{pull2}}\\[7mm] &\LARGE I_{Rf}+I_{Rpull2}=I_{Rs}　より、\\[5mm] &\LARGE \frac{V_{pull1}-V_a}{R_{pull1}+R_f}+\frac{V_{pull2}-V_{a}}{R_{pull2}}=\frac{V_a}{R_s}\\[13mm] \end{align*}

従って、Low→Hiの閾値は以下となります。

\begin{align*} &\LARGE V_a=\cfrac{ \cfrac{V_{pull2}}{R_{pull2}}+\cfrac{V_{pull1}}{R_{pull1}+R_f}}{{\cfrac{1}{R_{pull1}+R_f}+\cfrac{1}{R_{pull2}}+\cfrac{1}{R_s}}}\\[20mm] \end{align*}

入力信号がHi→Lowに変化する場合

入力信号がHi→Lowに変化する場合の閾値は、上記回路の場合は、Vout=GNDとすると、回路にVpull1の影響がありません。

したがって、(2)回路と同じ式となります。

\begin{align*} &\LARGE I_{Rf}=\frac{V_{out}-V_a}{R_f}\\[5mm] &\LARGE I_{Rs}=\frac{V_a}{R_s}\\[5mm] &\LARGE I_{Rpull2}=\frac{V_{pull2}-V_a}{R_{pull2}}\\[7mm] &\LARGE I_{Rs}+I_{Rpull2}=I_{Rs}　より、\\[5mm] &\LARGE \frac{V_{out}-V_a}{R_f}+\frac{V_{pull2}-V_a}{R_{pull2}}=\frac{V_a}{R_f}\\[13mm] \end{align*}

従って、Low→Hiの閾値は以下となります。

\begin{align*} &\LARGE V_a=\cfrac{ \cfrac{V_{out}}{R_f}+\cfrac{V_{pull2}}{R_{pull2}} }{\cfrac{1}{R_{pull2}}+\cfrac{1}{R_f}+\cfrac{1}{R_s}} \end{align*}

Vout=0としない場合は、この式を使用します。
ここで、VoutはGNDで飽和しているとすると、Vout=0

従って、Hi→Lowの閾値は、以下のようになります。

\LARGE V_a=V_{pull2}\cfrac{ \cfrac{R_fR_s}{R_f+R_s} }{R_{pull2}+\cfrac{R_fR_s}{R_f+R_s}}

Vout=Hiの場合

Voutは、出力がHiの場合、下記の計算式となります。
(Low側はVout=GNDとします)

\begin{align*} &\LARGE I_{Rf}=\frac{V_{out}-V_a}{R_f}\\[5mm] &\LARGE I_{Rpull1}=\frac{V_{pull1}-V_{out}}{R_{pull1}}\\[3mm] &\LARGE I_{Rs}=\frac{V_a}{R_s}\\[6mm] &\LARGE I_{Rpull2}=\frac{V_{pull2}-V_a}{R_{pull2}}\\[5mm] &\LARGE I_{Rf}=I_{Rpull1}　・・・(1)\\[3mm] &\LARGE I_{Rf}+I_{Rpull2}=I_{Rs}　・・・(2)\\[8mm] \end{align*}

(1)より

\begin{align*} &\LARGE \frac{V_{out}-V_a}{R_f}=\frac{V_{pull1}-V_{out}}{R_{pull1}}\\[3mm] &\LARGE V_a=V_{out}-(V_{pull1}-V_{out})\frac{R_f}{R_{pull1}}\\[8mm] &\LARGE V_a=\frac{V_{out}(V_{pull1}+R_f)-V_{pull1}R_f}{R_{pull1}}　・・・(3)\\[8mm] \end{align*}

(2)より

\begin{align*} &\LARGE \frac{V_{out}-V_a}{R_f}+\frac{V_{pull2}-V_a}{R_{pull2}}=\frac{V_a}{R_s}\\[3mm] &\LARGE \frac{V_{out}}{R_f}+\frac{V_{pull2}}{R_{pull2}}=V_a\Biggl({\cfrac{1}{R_{pull2}}+\cfrac{1}{R_f}+\cfrac{1}{R_s}}\Biggl)\\[13mm] \end{align*}

(3)を代入して、以下となります。

\begin{align*} &\LARGE V_{out}=\cfrac{ \cfrac{V_{pull1}R_f}{R_{pull1}}\Biggl({\cfrac{1}{R_{pull2}}+\cfrac{1}{R_f}+\cfrac{1}{R_s}}\Biggl)+\cfrac{V_{pull2}}{R_{pull2}}}{\cfrac{R_{pull1}+R_f}{R_{pull1}}\Biggl({\cfrac{1}{R_{pull2}}+\cfrac{1}{R_f}+\cfrac{1}{R_s}}\Biggl)-\cfrac{1}{R_f}}\\[15mm] \end{align*}

オープンコレクタ(4)

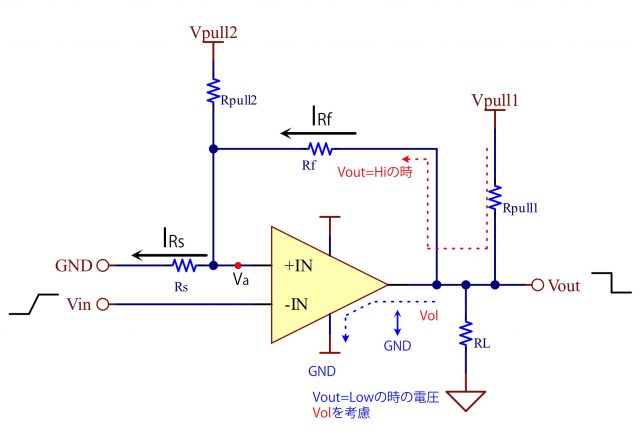
コンパレータ出力がLowの時の降下電圧を考慮した場合の計算を行ってみます。また、出力側のインピーダンスも考慮します。

入力信号がLow→Hiに変化する場合

入力信号がLow→Hiに変化する場合の閾値は、上記回路の場合、

\begin{align*} &\LARGE I_{pull1}=\frac{V_{pull1}-V_{out}}{R_{pull1}}\\[3mm] &\LARGE I_{RL}=\frac{V_{out}}{R_L}\\[7mm] &\LARGE I_{Rf}=\frac{V_{out}-V_a}{R_f}\\[3mm] &\LARGE I_{Rs}=\frac{V_a}{R_s}\\[7mm] &\LARGE I_{Rpull2}=\frac{V_{pull2}-V_a}{R_{pull2}}\\[7mm] &\LARGE I_{Rpull1}=I_{Rf}+I_{RL}\\[5mm] &\LARGE I_{Rs}=I_{Rpull2}+I_{Rf}\\[5mm] &\LARGE \frac{V_{pull1}-V_{out}}{R_{pull1}}=\frac{V_{out}-V_a}{R_f}+\frac{V_{out}}{R_L}　・・・(1)\\[8mm] &\LARGE \frac{V_a}{R_s}=\frac{V_{pull2}-V_a}{R_{pull2}}+\frac{V_{out}-V_a}{R_f}　・・・(2)\\[13mm] \end{align*}

(1)、(2)式を変形し、

\begin{align*} &\LARGE V_a=R_f\Biggl({\cfrac{V_{out}}{R_f}+\cfrac{V_{out}}{R_L}+\cfrac{V_{out}-V_{pull1}}{R_{pull1}}}\Biggl)　・・・(3)\\[8mm] &\LARGE V_{out}=R_f\Biggl({\cfrac{V_a}{R_s}-\cfrac{V_{pull2}-V_a}{R_{pull2}}+\cfrac{V_a}{R_f}}\Biggl)　・・・(4)\\[13mm] \end{align*}

(4)式を(3)式へ代入すると、Low→Hiの閾値は以下となります。

\begin{align*} &\LARGE V_a=\cfrac{ \cfrac{V_{pull2}}{R_{pull2}}\Biggl({R_f+\cfrac{R_f^{2}}{R_L}+\cfrac{R_f^{2}}{R_{pull1}}}\Biggl)+R_f\cfrac{V_{pull1}}{R_{pull1}}}{\Biggl({\cfrac{1}{R_{pull2}}+\cfrac{1}{R_f}+\cfrac{1}{R_s}}\Biggl)\Biggl({R_f+\cfrac{R_f^{2}}{R_L}+\cfrac{R_f^{2}}{R_{pull1}}}\Biggl)-1}\\[20mm] \end{align*}

入力信号がHi→Lowに変化する場合

入力信号がHi→Lowに変化する場合の閾値は、上記回路の場合は、Vout=Volとすると、回路にVpull1の影響がありません。

したがって、(2)回路と同じ式となります。

\begin{align*} &\LARGE I_{Rf}=\frac{V_{out}-V_a}{R_f}\\[5mm] &\LARGE I_{Rs}=\frac{V_a}{R_s}\\[7mm] &\LARGE I_{pull2}=\frac{V_{pull2}-V_a}{R_{pull2}}\\[7mm] &\LARGE I_{Rf}+I_{Rpull2}=I_{Rs}　より、\\[7mm] &\LARGE \frac{V_{out}-V_a}{R_f}+\frac{V_{pull2}-V_a}{R_{pull2}}=\frac{V_a}{R_s}\\[10mm] \end{align*}

従って、Hi→Lowの閾値は以下となります。

\begin{align*} &\LARGE V_a=\cfrac{ \cfrac{V_{out}}{R_f}+\cfrac{V_{pull2}}{R_{pull2}} }{\cfrac{1}{R_{pull2}}+\cfrac{1}{R_f}+\cfrac{1}{R_s}}\\[20mm] \end{align*}

Vout=Hiの場合

Voutは、出力がHiの場合、下記の計算式となります。

\begin{align*} &\LARGE I_{Rpull1}=\frac{V_{pull1}-V_{out}}{R_{pull1}}\\[3mm] &\LARGE I_{RL}=\frac{V_{out}}{R_L}\\[7mm] &\LARGE I_{Rf}=\frac{V_{out}-V_a}{R_f}\\[5mm] &\LARGE I_{Rs}=\frac{V_a}{R_s}\\[8mm] &\LARGE I_{Rpull2}=\frac{V_{pull2}-V_a}{R_{pull2}}\\[8mm] &\LARGE I_{Rpull1}=I_{Rf}+I_{RL}\\[5mm] &\LARGE I_{Rs}=I_{Rpull2}+I_{Rf}\\[10mm] &\LARGE \frac{V_{pull1}-V_{out}}{R_{pull1}}=\frac{V_{out}-V_a}{R_f}+\frac{V_{out}}{R_L}　・・・(1)\\[8mm] &\LARGE \frac{V_a}{R_s}=\frac{V_{pull2}-V_a}{R_{pull2}}+\frac{V_{out}-V_a}{R_f}　・・・(2)\\[10mm] \end{align*}

(1),(2)式を変形し、

\begin{align*} &\LARGE V_{out}=\cfrac{ \cfrac{V_a}{R_f}+\cfrac{V_{pull1}}{R_{pull1}}}{{\cfrac{1}{R_{pull1}}+\cfrac{1}{R_f}+\cfrac{1}{R_L}}}　・・・(3)\\[18mm] &\LARGE V_a=\cfrac{ \cfrac{V_{pull2}}{R_{pull2}}+\cfrac{V_{out}}{R_f}}{{\cfrac{1}{R_{pull2}}+\cfrac{1}{R_f}+\cfrac{1}{R_s}}}　・・・(4)\\[20mm] \end{align*}

(4)式を(3)式へ代入すると、以下となります。

\begin{align*} &\LARGE V_{out}=\cfrac{ \cfrac{V_{pull1}R_f}{R_{pull1}}\Biggl({\cfrac{1}{R_{pull2}}+\cfrac{1}{R_f}+\cfrac{1}{R_s}}\Biggl)+\cfrac{V_{pull2}}{R_{pull2}}}{\Biggl({\cfrac{R_f}{R_L}+\cfrac{R_{pull1}+R_f}{R_{pull1}}}\Biggl)\Biggl({\cfrac{1}{R_{pull2}}+\cfrac{1}{R_f}+\cfrac{1}{R_s}}\Biggl)-\cfrac{1}{R_f}}\\[20mm] \end{align*}

おわりに

Cerevo社内でコンパレータが話題が出たのをきっかけに、数年前に作った資料の存在を思い出したので、筆を執ってみました。迷える方の参考になれば幸いです。

途中計算を省いているので、分かりづらい等あればご意見いただければと思います。理解出来てるよという猛者の方は暇つぶしに検算してみてはいかがでしょうか。もしかしたら記述ミスがみつかるかも(…)。

エンジニア積極採用中

現在Cerevoでは各種エンジニアの採用、またハードウェア共同開発・受託開発を絶賛募集しております。それぞれご関心お持ちいただける方は、以下の専用お問い合わせフォームよりご連絡お待ちしております。

現在募集している職種
https://cerevo.com/recruit/
　
ハードウェア共同開発および受託開発のご相談
https://cerevo.com/contact/sales/

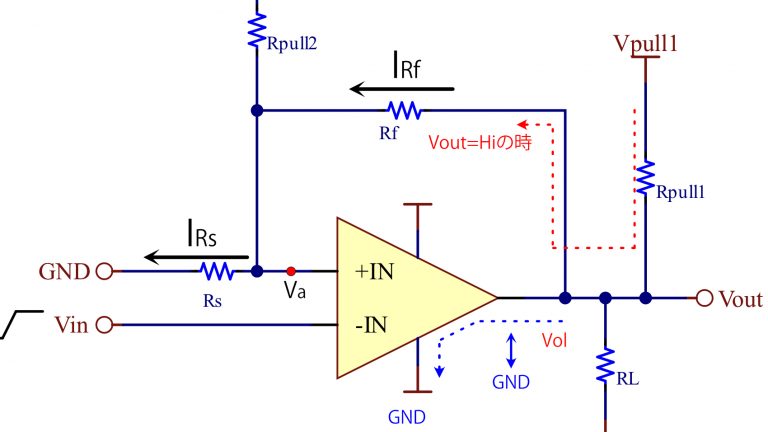オペアンプを用いたコンパレータ動作時におけるヒステリシス回路の考え方