こんにちは。こんばんは。おはようございます。おやすみなさい。
電気エンジニアのyokoyamaです。
オペアンプには、入力バイアス電流というものが存在します。
通常、理想のオペアンプとして仮定され、入力バイアス電流 = 0と考えます。
しかし、実際はどうなのか?
ということで、回路の動作にどう影響するのかを書いてみたいと思います。
目次
おさらい・オペアンプとは
オペアンプとは、微弱な電気信号を増幅することができる集積回路です。
前回、オペアンプを用いたコンパレータ回路についての記事を書きましたが、オペアンプはコンパレータだけでなく、増幅回路、積分回路、発振回路など様々な回路に応用されています。
入力バイアス電流について
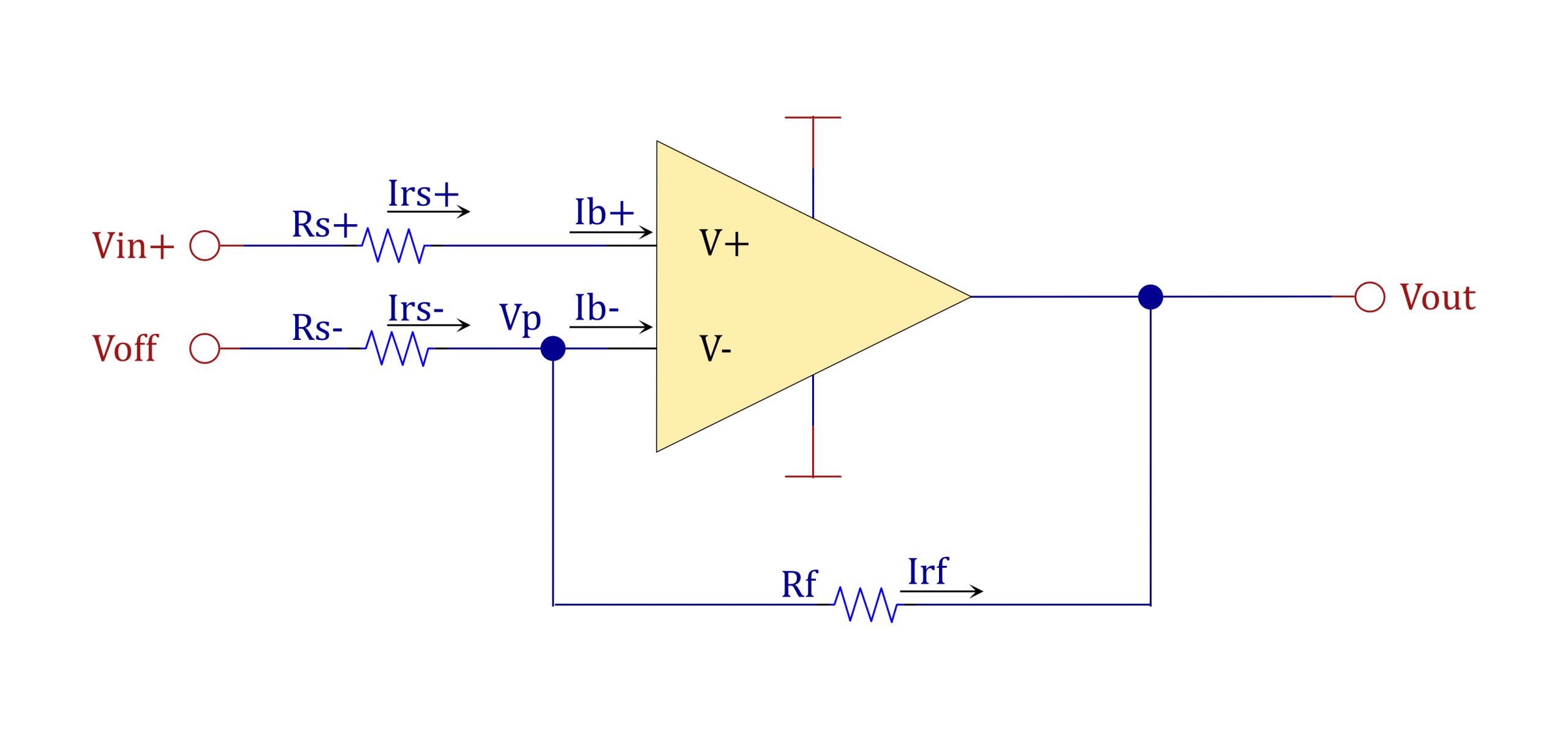
入力バイアス電流とは、オペアンプに流れ込む(または流れ出てくる)微量な電流のことです。
(図中 I_{b+}, I_{b-})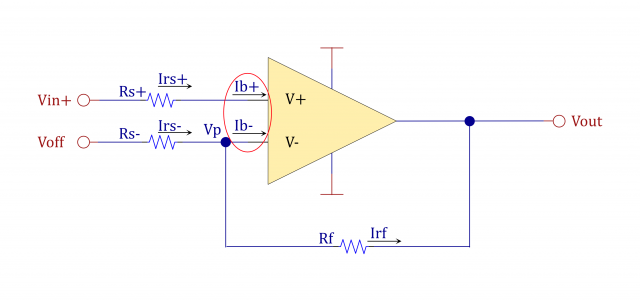
通常、数pA~数uAという微量な電流であるため、設計時には考慮しないことが多いと思います。
しかし……無視できない場合があり、無視できない例を紹介していきます。
オペアンプのV+端子側バイアス電流が無視できない例
その1
\begin{align*}
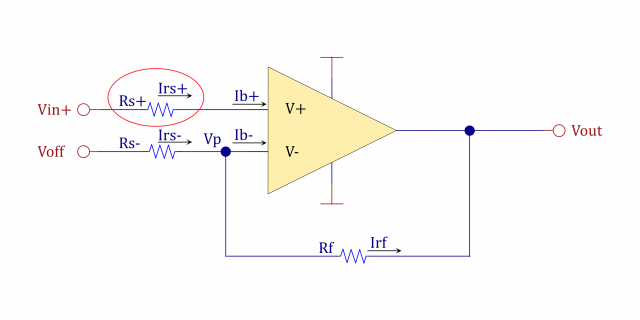
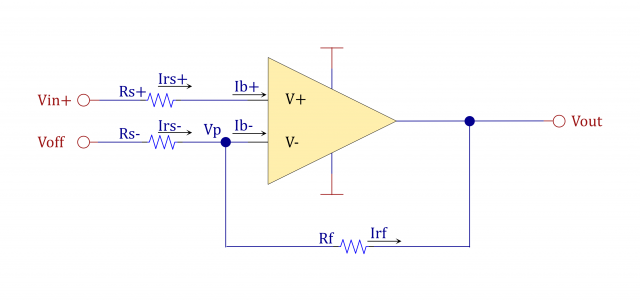
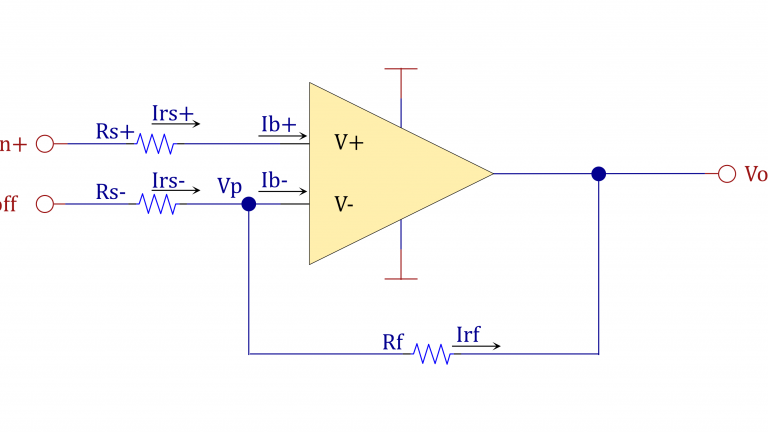
&非反転増幅回路ですが、本によってはR_{s+}が省略されていることも多いですね。\\
&理想オペアンプであればR_{s+}の影響がないからです。\\
&しかし、実はこれの抵抗値を適切に選ばないとバイアス電流の存在にによって発生するオフセット電圧が大きくなってしまいます。\\
&これについて考察していきます。\\[5mm]
&\large V+端子に挿入する抵抗が大きければバイアス電流が出力に与える影響も大きくなります。\\
& 信号源のインピーダンスが高い場合にこれと同じことが起きてしまう場合もありますね。\\[5mm]
&R_{s-} = 1kΩ, R_f = 1kΩ, R_{s+} = 10kΩ, I_b = 1uAとすると、\\[5mm]
&\left( \frac{R_f}{R_{s-}} + 1 \right) I_bR_{s+}
\normalsize(※)より、\\[5mm]
&ゲイン倍されて200mVという 思いのほか大きなオフセットとして現れます。\\[5mm]
&以下、上記※式について求めます。\\[5mm]
& I_{rs+} = \frac{V_{in} - V_p}{R_{s+}} = I_{b+} \hspace{10mm} ・・・(1)\\[5mm]
& I_{rs-} = \frac{V_{off} - V_p}{R_{s-}} \hspace{5mm} ・・・(2)\\[5mm]
& I_{rf} = \frac{V_p - V_{out}}{R_f} \hspace{5mm} ・・・(3)\\[5mm]
& I_{rf} = I_{rs-} - I_{b-} \hspace{5mm} ・・・(4)\\[5mm]
&(1)より、\\[5mm]
& -V_p = I_{b+}R_S - V_{in}\\[5mm]
& V_p = V_{in} - I_{b+}R_{s+} \hspace{5mm} ・・・(5)\\[5mm]
&(4)より、\\[5mm]
& \frac{V_p - V_{out}}{R_f} = \frac{V_{off} - V_p}{R_{s-}} -
I_{b-}\\[5mm]
& V_{out} = \left(\frac{R_f}{R_{s-}} + 1 \right) V_p - \frac{R_f}{R_{s-}} V_{off} + R_fI_{b-}\\[10mm]
&(5)を代入して、\\[5mm]
&V_{out} = \left(\frac{R_f}{R_{s-}} + 1 \right) (V_{in} - I_{b+}R_{s+}) - \frac{R_f}{R_{s-}} V_{off} + R_fI_{b-}\\[5mm]
& ここで、オフセット電圧のみを考慮するため V_{off} = 0, \\
& オペアンプの+入力、-入力のバイアス電流が等しいと仮定して I_{b+} = I_{b-} = I_b \normalsizeとすると、\\[5mm]
& V_{out} = \left(\frac{R_f}{R_{s-}} + 1 \right) (V_{in} - I_bR_{s+}) + R_fI_b\\[5mm]
& = \left(\frac{R_f}{R_{s-}} + 1 \right) V_{in} - \left(\frac{R_f}{R_{s-}} + 1 \right)I_bR_{s+} + R_fI_b\\[5mm]
&\footnotesize第1項・・・ゲイン項\\
&\footnotesize第2項・・・V+側の影響(※)\\
&\footnotesize第3項・・・V-側の影響\\
\end{align*}その2
\begin{align*}
&I_{b+} = I_{b-}, R_{s+} = R_{s-}としても、R_s = 10kΩ, I_b = 1uAならオフセットは I_bR_s(※) \normalsizeより、10mVとなり、完全には消えません。\\
&(しかし、その1に比べるとかなり改善します。)\\[5mm]
&以下、上記※式について求めます。\\
&といっても、式(5)を代入した形までは同じです。\\[5mm]
& V_{off} = 0,\hspace{2mm} R_{s+} = R_{s-} = R_s, \hspace{2mm}I_{b+} = I_{b-} = I_b \normalsizeとすると、\\[5mm]
& V_{out} = \left(\frac{R_f}{R_s} + 1 \right) (V_{in} - I_bR_s) + R_fI_b\\[5mm]
& = \frac{R_f}{R_s} (V_{in} - I_bR_s) + V_{in} - I_bR_s + R_fI_b\\[5mm]
& = \frac {R_f}{R_s} V_{in} + V_{in}
-I_bR_s\\[5mm]
& = \left( 1 + \frac {R_f}{R_s} \right) V_{in} - I_bR_s//\\[5mm]
&\footnotesize第1項・・・ゲイン項\\
&\footnotesize第2項・・・オフセット項(バイアス)\\[5mm]
&R_{s+} = R_{s-}としても、バイアス電流の影響が残ります。\\[5mm]
\end{align*}対策してみる
オペアンプを変えずにバイアス電流をキャンセルする
\begin{align*}
& R_{s+} = R_{s-}としたくなるところですが、実はR_{s+} = R_{s+} // R_f = \frac{R_f R_{s-}}{R_f + R_{s-}}\\
& 要はR_{s+} を R_{s-} の並列抵抗値として選ぶことでバイアス電流による\\
& オフセットをキャンセルすることができます。\\
& これも実際に計算してみましょう。\\
& さきほどまでの例で回路解析は終わってますから、これに代入して確かめてみます。\\[5mm]
& V_{out} = \left(\frac{R_f}{R_{s-}} + 1 \right) V_{in} - \left(\frac{R_f}{R_{s-}} + 1 \right)I_bR_{s+} + R_fI_b\\[10mm]
& 第2項、第3項が0になる条件について考えてみます。\\[5mm]
& R_fI_b = \left(\frac{R_f}{R_{s-}} + 1 \right)I_bR_{s+}\\[5mm]
& R_sについて解くと、\\[5mm]
& R_{s+} = \frac{R_f R_{s-}}{R_f + R_{s-}}\\[10mm]
& が得られますね。\\[10mm]
\end{align*}\begin{align*}
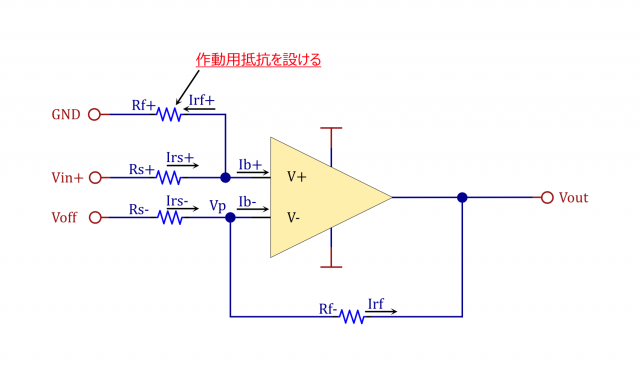
& このほか、このように抵抗を1本追加する対策方法もあります。\\[5mm]
& I_{rs+} = \frac{V_{in} - V_p}{R_{s+}} = I_{b+} + I_{rf+}\hspace{5mm} ・・・(1)\\[5mm]
& I_{rs-} = \frac{V_{off} - V_p}{R_{s-}} \hspace{5mm} ・・・(2)\\[5mm]
& I_{rf-} = \frac{V_p - V_{out}}{R_{f-}} \hspace{5mm} ・・・(3)\\[5mm]
& I_{rf-} = I_{rs-} - I_{b-} \hspace{5mm} ・・・(4)\\[5mm]
& I_{rf+} = \frac{V_p}{R_{f+}} \hspace{5mm} ・・・(5)\\[10mm]
& (1)(5)より、 \\[5mm]
& \frac{V_{in} - V_p}{R_{s+}} = I_{b+} + \frac{V_p}{R_{f+}} \hspace{10mm} \\[15mm]
&***途中式割愛❤*** \\[10mm]
& V_p = \frac{R_{f+}} {R_{f+} + R_{s+}}(V_{in} - I_{b+}R_{s+}) \hspace{5mm} ・・・(6)\\[10mm]
&(4)より\\[5mm]
& \frac{V_p - V_{out}} {R_{f-}} = \frac{V_{off} - V_p} {R_{s-}}-I_{b-} \hspace{10mm} \\[5mm]
& V_{out} = \left( \frac {R_{f-}}{R_{s-}} + 1 \right) V_{p} - \frac {R_{f-}}{R_{s-}} V_{off} + R_{f-}I_{b-}\\[10mm]
&(6)を代入して\\[5mm]
& V_{out} = \left( \frac {R_{f-}}{R_{s-}} + 1 \right) \left ( \frac{R_{f+}} {R_{f+} + R_{s+}}(V_{in} - I_{b+}R_{s+}) \right) - \frac {R_{f-}}{R_{s-}} V_{off} + R_{f-}I_{b-} \hspace{5mm} \\[10mm]
&ここで、\\[5mm]
&V_{off} = 0, R_{s-} = R_{s+}, I_{b+} = I_{b-} = I_b, R_{f+} = R_{f-} = R_{f}\\[5mm]
&とすると、\\[5mm]
& V_{out} = \left( \frac {R_{f}}{R_{s}} + 1 \right) \left ( \frac{R_{f}} {R_{f} + R_{s}}(V_{in} - I_{b}R_{s}) \right) + R_{f}I_{b} \hspace{5mm} \\[10mm]
& = \frac {R_{f}}{R_{s}} \frac{R_{f}} {R_{f} + R_{s}}(V_{in} - I_{b}R_{s}) \frac{R_{f}} {R_{f} + R_{s}}(V_{in} - I_{b}R_{s}) + R_{f}I_{b} \hspace{5mm} \\[15mm]
&***途中式割愛❤*** \\[10mm]
& = V_{in} \left(\frac {R_{f}(R_f+R_s)}{R_{s}(R_f+R_s)}\right) - I_{b}R_{s} \left(\frac {R_{f}(R_f+R_s)}{R_{s}(R_f+R_s)}\right) + R_{f}I_{b} \hspace{5mm} \\[4mm]
&\footnotesize第1項・・・ゲイン項\\
&\footnotesize第2,3項・・・オフセット項(バイアス)\\[5mm]
& = V_{in} \frac {R_{f}}{R_{s}} - R_{f}I_{b} + R_{f}I_{b}\hspace{5mm} \\[10mm]
&\left \{ \begin{array}{l} R_{s+} = R_{s-}\\
R_{f+} = R_{f-}\\
\end{array} \right. \\[5mm]
&と設定すると、出力電圧は、 V_{in}\frac{R_f}{R_s} のみとなり、\\[5mm]
&バイアス電流I_bの影響がキャンセルできました! \end{align*}入力にフィルタ用コンデンサを追加するとどうなるか
\begin{align*}
& さて、ここまでは入力バイアス電流による出力オフセット電圧への影響を考えてきました。\\
& 今度は違う切り口でバイアス電流による影響を見ていきたいと思います。\\
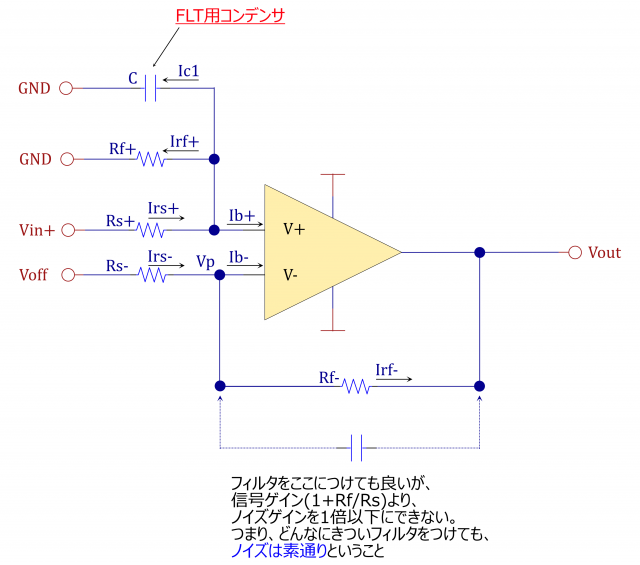
& 実際にオペアンプ回路を組む時、オペアンプの入力にノイズの除去などを目的とした次のようなCRフィルタを入れたい場合があります。\\
& 実は、これの効果にもオペアンプの入力バイアス電流が関係してきます。\\[5mm]
& I_{rs+} = \frac{V_{in} - V_p}{R_{s+}} = I_{b+} + I_{rf+} + I_{C1} \hspace{5mm} ・・・(1)\\[5mm]
& I_{rs-} = \frac{V_{off} - V_p}{R_{s-}} \hspace{5mm} ・・・(2)\\[5mm]
& I_{rf-} = \frac{V_p - V_{out}}{R_{f-}} \hspace{5mm} ・・・(3)\\[5mm]
& I_{rf-} = I_{rs-} - I_{b-} \hspace{5mm} ・・・(4)\\[5mm]
& I_{rf+} = \frac{V_p}{R_{f+}} \hspace{5mm} ・・・(5)\\[5mm]
& I_{C1} = sCV_p \hspace{5mm} ・・・(6)\\[4mm]
& \footnotesize ※sCV_pの"s"はラプラス変換子\\[5mm]
& (1)(5)(6)より、\\[5mm]
& \frac{V_{in} - V_p}{R_{s+}} = I_{b+} + \frac{V_p}{R_{f-}} + sCV_p \hspace{5mm} \\[10mm]
&***途中式割愛❤*** \\[10mm]
& V_p = \frac{1} {\frac{1} {R_{f+}} + \frac{1} {R_{s+}} +sC } \left( \frac {V_{in}} {R_{s+}} - I_{b+} \right) ・・・(7)\\[10mm]
& (4)より、\\[5mm]
& \frac{V_p - V_{out}}{R_{f-}} = \frac{V_{off} - V_p}{R_{s-}} - I_{b-}\\[5mm]
& V_{out} = \left( \frac {R_{f-}}{R_{s-}} + 1 \right) V_p - \frac{R_{f-}}{R_{s-}} V_{off} + R_{f-} I_{b-} \hspace{5mm} \\[10mm]
& (7)を代入して、\\[5mm]
& V_{out} = \left( \frac {R_{f-}}{R_{s-}} + 1 \right) \frac{1} {\frac{1} {R_{f+}} + \frac{1} {R_{s+}} +sC } \left( \frac {V_{in}} {R_{s+}} - I_{b+} \right) - \frac{R_{f-}}{R_{s-}} V_{off} + R_{f} I_{b-} \hspace{5mm} \\[10mm]
&ここで、\\[5mm]
&V_{off} = 0, R_{s-} = R_{s+} = R_{s}, I_{b+} = I_{b-} = I_b, R_{f+} = R_{f-} = R_{f}\\[5mm]
&とすると、\\[5mm]
& V_{out} = \left( \frac {R_{f}}{R_{s}} + 1 \right) \frac{1} {\frac{1} {R_{f}} + \frac{1} {R_{s}} +sC } \left( \frac {V_{in}} {R_{s}} - I_{b} \right) - R_{f} I_{b} \hspace{5mm} \\[10mm]
& = \left( \frac {R_{f}}{R_{s}} + 1 \right) \frac{R_f R_S} { R_{s} + R_f + sCR_sR_f } \left( \frac {V_{in}} {R_{s}} - I_{b} \right) + R_{f} I_{b} \hspace{5mm} \\[15mm]
&***途中式割愛❤*** \\[10mm]
& = V_{in} \frac {R_{f}} {R_{s}} \left( \frac{R_f + R_S} { R_{s} + R_f + sCR_sR_f }\right) - R_fI_b \left( \frac{R_f + R_S} { R_{s} + R_f + sCR_sR_f }\right) +R_fI_b \hspace{5mm} \\[20mm]
& ※V_{out} = V_{in} \frac {R_{f}}{R_{s}} \left( \frac{R_f + R_S} { R_{s} + R_f + sCR_sR_f }\right) - R_fI_b \left( \frac{R_f + R_S} { R_{s} + R_f + sCR_sR_f }\right) +R_fI_b//
\hspace{5mm} \\[4mm]
&\footnotesize第1項・・・ゲイン項\\
&\footnotesize第2項・・・オフセット項(バイアス)\\[5mm]
&となります。\\[5mm]
&ここで、両項ともにでてきているsCR_sR_fが周波数依存部になります。\\[5mm]
&\fbox{低周波領域では、} \\[5mm]
& 最終値の定理からs → 0より、\\[5mm]
& V_{out} = V_{in} \frac {R_{f}}{R_{s}} \left( \frac{R_f + R_S} { R_{s} + R_f + 0 }\right) - R_fI_b \left( \frac{R_f + R_S} { R_{s} + R_f + 0 }\right) +R_fI_b
\hspace{5mm} \\[5mm]
& = V_{in} \frac {R_{f}}{R_{s}} - R_fI_b +R_fI_b
\hspace{5mm} \\[5mm]
& = V_{in} \frac {R_{f}}{R_{s}}\hspace{5mm} \\[5mm]
&出力電圧は、 V_{in}\frac{R_f}{R_s}\\[5mm]
&のみとなり、オフセットがキャンセルされました。\\
& 前節と同じようにR_{f+}の効果でオフセット電圧は現れていません。\\
&それでは、フィルタとしての効果を期待している高周波領域ではどうでしょうか。\\[10mm]
&\fbox{高周波領域では、} \\[5mm]
& 初期値の定理からs → ∞より、\\[5mm]
& V_{out} = V_{in} \frac {R_{f}}{R_{s}} \left( \frac{R_f + R_S} { R_{s} + R_f + ∞ }\right) - R_fI_b \left( \frac{R_f + R_S} { R_{s} + R_f + ∞ }\right) + R_fI_b
\hspace{5mm} \\[5mm]
& = R_fI_b \hspace{5mm} \\[5mm]
&出力電圧は、 R_fI_bと、オフセットのみ残ります。\\
&ノイズ成分もバイアス電流と関係して現れるということです。\\
&バイアス電流と関係して現れる入力段のみにCを入れる場合、低周波領域では良好な結果が得られるものの、 \\
&信号が高周波であったりノイズが多い場合、期待したフィルタ効果が得られないことになります。 \\
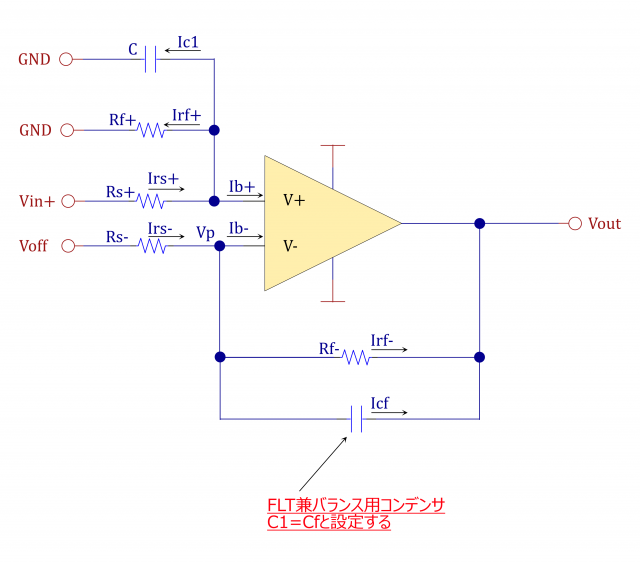
\end{align*}FB部にもコンデンサを追加
\begin{align*}
& I_{rs+} = \frac{V_{in} - V_p}{R_{s+}} = I_{b+} + I_{rf+} + I_{C1} \hspace{5mm} ・・・(1)\\[5mm]
& I_{rs-} = \frac{V_{off} - V_p}{R_{s-}} \hspace{5mm} ・・・(2)\\[5mm]
& I_{rf-} = \frac{V_p - V_{out}}{R_{f-}} \hspace{5mm} ・・・(3)\\[5mm]
& I_{rf-} = I_{rs-} - I_{b-} - I_{Cf} \hspace{5mm} ・・・(4)\\[5mm]
& I_{rf+} = \frac{V_p}{R_{f+}} \hspace{5mm} ・・・(5)\\[5mm]
& I_{C1} = sC_1V_p \hspace{5mm} ・・・(6)\\[4mm]
& I_{Cf} = sC_f(V_p - V_{out}) \hspace{5mm} ・・・(7)\\[4mm]
& (1)(5)(6)より、\\[5mm]
& \frac{V_{in} - V_p}{R_{s+}} = I_{b+} + \frac{V_p}{R_{f+}} + sC_1V_p \hspace{5mm} \\[10mm]
&***途中式割愛❤*** \\[10mm]
& V_p = \frac{1} {\frac{1} {R_{f+}} + \frac{1} {R_{s+}} +sC_1 } \left( \frac {V_{in}} {R_{s+}} - I_{b+} \right) ・・・(8)\\[10mm]
& (4)より、\\[5mm]
& \frac{V_p - V_{out}}{R_{f-}} = \frac{V_{off} - V_p}{R_{s-}} - I_{b-} -sC_f (V_p - V_{out})\\[10mm]
&***途中式割愛❤*** \\[10mm]
&V_{out} = \frac{1} {-\frac{1} {R_{f-}} - sC_f }
\left( \frac{V_{off}} {R_{s-}} - \frac{V_p} {R_{s-}} - sC_fV_p
- \frac{V_p} {R_{f-} - I_{b-}} \right)\\[10mm]
& = \frac {V_{off}} {R_{s-}}
\frac{1}
{-\frac{1} {R_{f-}} - sC_f }
+V_p
\frac{ \left( \frac{1} {R_{f-}} + \frac{1} {R_{s-}} + sC_f
\right)}
{\left(\frac{1} {R_{f-}} + sC_f\right)}
+ I_{b-}
\frac{1}
{\left( \frac{1} {R_{f-}} + sC_f \right)} \\[10mm]
& (8)を代入して、\\[5mm]
& = \frac {V_{off}} {R_{s-}}
+
\frac{1} {\frac{1} {R_{f+}} + \frac{1} {R_{s+}} +sC_1 }
\left( \frac {V_{in}} {R_{s+}} - I_{b+} \right)
\frac{ \left( \frac{1} {R_{f-}} + \frac{1} {R_{s-}} + sC_f
\right)}
{\left(\frac{1} {R_{f-}} + sC_f\right)}
+ I_{b-}
\frac{1}
{\left( \frac{1} {R_{f-}} + sC_f \right)} \\[10mm]
&ここで、\\
&V_{off} = 0, R_{s-} = R_{s+} = R_{s}, I_{b+} = I_{b-} = I_b, R_{f+} = R_{f-} = R_{f}, C_1 = C_f = C\\
&とすると、 \\[5mm]
& =
\frac{1} {\frac{1} {R_{f}} + \frac{1} {R_{s}} +sC }
\left( \frac {V_{in}} {R_{s}} - I_{b} \right)
\frac{ \left( \frac{1} {R_{f}} + \frac{1} {R_{s}} + sC
\right)}
{\left(\frac{1} {R_{f}} + sC\right)}
+ I_{b}
\frac{1}
{\left( \frac{1} {R_{f}} + sC \right)} \\[10mm]
& =
\frac{V_{in}} {R_{s}}
\frac{1} {\left( \frac{1} {R_{f}} +sC \right)}
- I_{b}
\frac{1}
{\left( \frac{1} {R_{f}} + sC \right)}
+ I_{b}
\frac{1}
{\left( \frac{1} {R_{f}} + sC \right)}\\[10mm]
& =
\frac{V_{in}} {R_{s}}
\frac{1} {\left( \frac{1} {R_{f}} +sC \right)} \\[5mm]
&\footnotesize第1項・・・ゲイン項\\
&\footnotesize第2項・・・オフセット項(バイアス)\\[5mm]
&入力段とFB部の両方にコンデンサを追加すると、
バイアス電流による影響がキャンセルされました。\\[5mm]
& この式、V_{out} =
\frac{V_{in}} {R_{s}}
\frac{1} {\left( \frac{1} {R_{f}} +sC \right)}の意味ですが、 \\[10mm]
&\fbox{低周波領域では、} \\[5mm]
& s → 0より、\\[5mm]
& V_{out} =
\frac{V_{in}} {R_{s}}
\frac{1} {\left( \frac{1} {R_{f}} + 0 \right)}
\hspace{5mm} \\[5mm]
& =
\frac{V_{in}} {R_{s}} \frac{1} {\frac{1}{R_f}}\\[5mm]
& =
V_{in}\frac{R_f} {R_{s}} \\[10mm]
&\fbox{高周波領域では、} \\[5mm]
& s → ∞より、\\[5mm]
& V_{out} =
\frac{V_{in}} {R_{s}}
\frac{1} {\left( \frac{1} {R_{f}} + ∞ \right)}
\hspace{5mm} \\[5mm]
& =
\frac{V_{in}} {R_{s}} \frac{1}{∞}\\[5mm]
& =
\frac{V_{in}} {R_{s}} ・0\hspace{5mm} \\[5mm]
& =
0\hspace{5mm} \\[5mm]
&低周波領域では、信号を増幅し、高周波領域では、信号をカットされています。\\
&つまり、LPFになっています。
\end{align*}おまけ
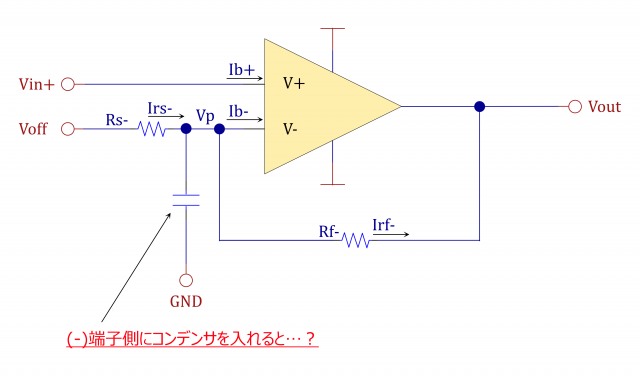
危険なコンデンサ
\begin{align*}
& 一見、LPFになるように見えますが…?\\[5mm]
& I_{rs-} = \frac{V_{off} - V_p}{R_{s-}} \hspace{5mm} ・・・(1)\\[5mm]
& I_{rf-} = \frac{V_p - V_{out}}{R_{f-}} \hspace{5mm} ・・・(2)\\[5mm]
& I_{c} = sCV_p \hspace{5mm} ・・・(3)\\[4mm]
& I_{rf-} = I_{rs-} - I_C - I_{b-} \hspace{5mm} ・・・(4)\\[4mm]
&(4)より、\\[5mm]
& \frac{V_p - V_{out}}{R_{f-}}
=
\frac{V_{off} - V_p}{R_{s-}}
-
sCV_p - I_{b-}\\[5mm]
& \frac{V_p}{R_{f-}} - \frac{V_{out}}{R_{f-}}
=
\frac{V_{off}}{R_{s-}} - \frac{V_p}{R_{s-}} - sCV_p - I_{b-}\\[5mm]
& -\frac{V_{out}}{R_{f-}} = \frac{V_{off}}{R_{s-}}
-
\frac{V_p}{R_{f-}} - \frac{V_p}{R_{s-}} - sCV_p - I_{b-}\\[5mm]
& -V_{out} =
R_{f-}\frac{V_{off}}{R_{s-}}
- V_p
\left( 1+ \frac{R_{f-}}{R_{s-}} + sR_{f-}C_1 \right) - I_{b-}R_{f-}\\[5mm]
& V_p = V_{in}, V_{off} = 0, I_{b-} = 0とすると、\\[5mm]
& V_{out} =
V_{in}
\left( 1+ \frac{R_{f-}}{R_{s-}} + sR_{f-}C_1 \right) \\[10mm]
&\fbox{高周波領域では、} \\[5mm]
& s → ∞より、\\[5mm]
& V_{out} =
V_{in}
\left( 1+ \frac{R_{f-}}{R_{s-}} + ∞ \right) \\[5mm]
& = ∞ \\[5mm]
& ということで、ここのコンデンサは、Vinに対してHPFになってしまい、ノイズを増幅してしまいます。
\end{align*}おわりに
今回はオペアンプの入力バイアス電流についてまとめてみました。
いかがでしたか?(某まとめ系サイトの終わり方)
入力バイアス電流も以外とバカにならないことが分かって頂けたかと思います。
設計時の参考になれば幸いです。
次回は実際に回路を組んで同様の結果を得られるか試してみる実験を行ってみたいと思います。
エンジニア積極採用中
現在Cerevoでは各種エンジニアの採用、またハードウェア共同開発・受託開発を絶賛募集しております。それぞれご関心お持ちいただける方は、以下の専用お問い合わせフォームよりご連絡お待ちしております。
- 現在募集している職種
https://cerevo.com/recruit/
- ハードウェア共同開発および受託開発のご相談
https://cerevo.com/contact/
著者プロフィール

- Cerevo 電気エンジニア
最近の投稿
 01. ハードウェア2022.04.01オペアンプバイアス電流によるオフセット電圧の影響を考える
01. ハードウェア2022.04.01オペアンプバイアス電流によるオフセット電圧の影響を考える 01. ハードウェア2021.10.19オペアンプを用いたコンパレータ動作時におけるヒステリシス回路の考え方
01. ハードウェア2021.10.19オペアンプを用いたコンパレータ動作時におけるヒステリシス回路の考え方 資格試験2021.07.26第2種電気工事士 技能試験を電気エンジニアが受けるときに押さえたポイント
資格試験2021.07.26第2種電気工事士 技能試験を電気エンジニアが受けるときに押さえたポイント 資格試験2021.06.01電気エンジニアがした第2種電気工事士、筆記試験の対策ポイント
資格試験2021.06.01電気エンジニアがした第2種電気工事士、筆記試験の対策ポイント