はじめに
こんにちは。電気エンジニアの早川です。
前回、ディジタルフィルタのうちFIRフィルタについての解説を行いました。
今回は主にIIRフィルタについて解説したいと思います。
IIRフィルタはアナログフィルタとの共通点が多く、本記事ではここに着目しながらアナログフィルタとディジタルフィルタの深い関係性に触れていきます。
目次
ブロック線図によるフィルタの表現
フィルタを理解する上で大きな手助けとなるのがその構造を表すブロック線図という表現です。まずは簡単なFIRフィルタの例から解説します。
FIRフィルタのブロック線図
FIRフィルタをブロック線図で表現すると次のようになります。
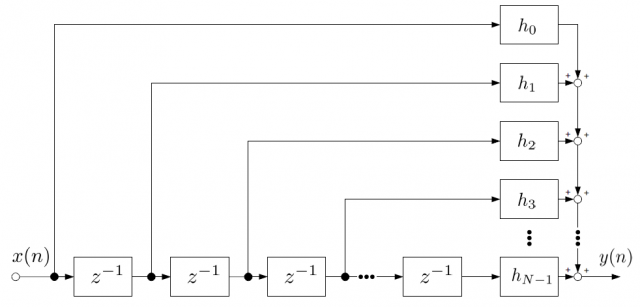
ここで、z^-1は入力を1サンプル遅延させる働きを持つ、遅延素子です。
これはz変換による表現ですが、z変換自体の意味はさほど考えなくても実用上問題ありません。z^-1が1サンプルの遅延をもたらすということだけ考えれば十分です。電気回路の解析でjωの意味を深く考えなくても支障がないのと同じです。
FIRフィルタのアルゴリズムは、入力をインパルス列と考えると、それを時間シフトしたものにインパルス応答を掛け算してその総和を取るというものでした。この図からも、そのアルゴリズムがひと目でわかります。
FIRフィルタの実現方法にはいくつかの種類がありますが、これが最もシンプルな実現方法です。
FIRフィルタの伝達関数
ブロック線図で表現すると伝達関数の計算が簡単になります。この場合、次式になりますね。
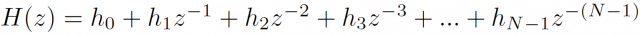
IIRフィルタのブロック線図
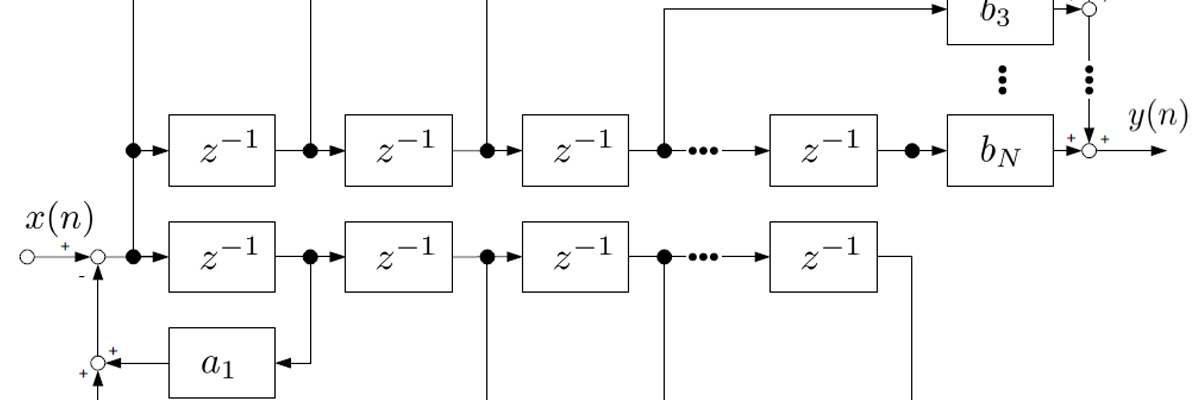
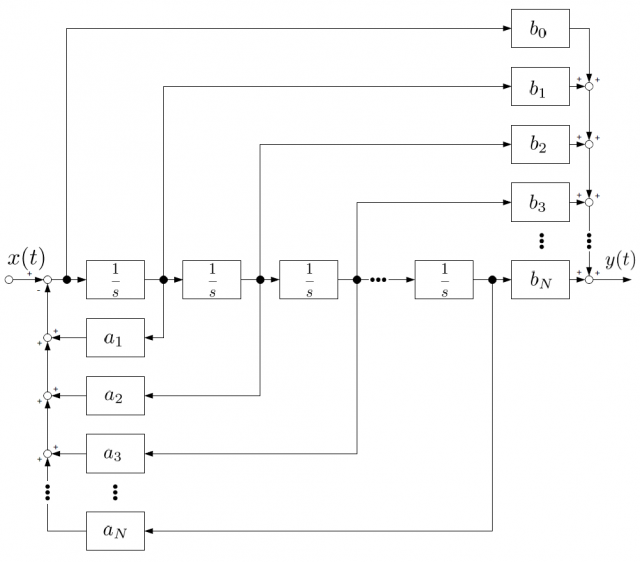
IIRフィルタはどうでしょうか。いろいろな構成がありますが、次のようなものが最もシンプルです。これは直接型IIとよばれる構成です。
上半分はFIRフィルタと同じ構造ですが、下半分を見るとフィードバックが追加されていることがわかります。これがFIRフィルタとIIRフィルタの最大の違いです。
IIRフィルタの伝達関数
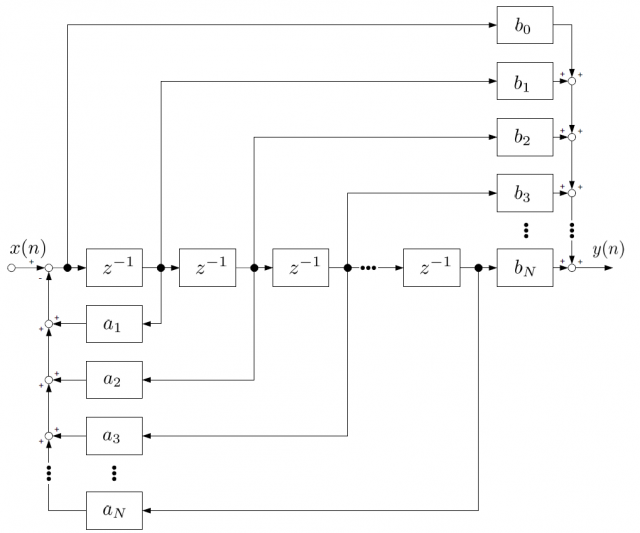
こちらも伝達関数を計算してみます。ブロック線図を上半分と下半分に分けると考えやすいので、次のような等価変換を行ってみます。
こうすると、上半分はFIRフィルタと全く同じ形をしていますからこの部分の伝達関数の計算は簡単ですね。
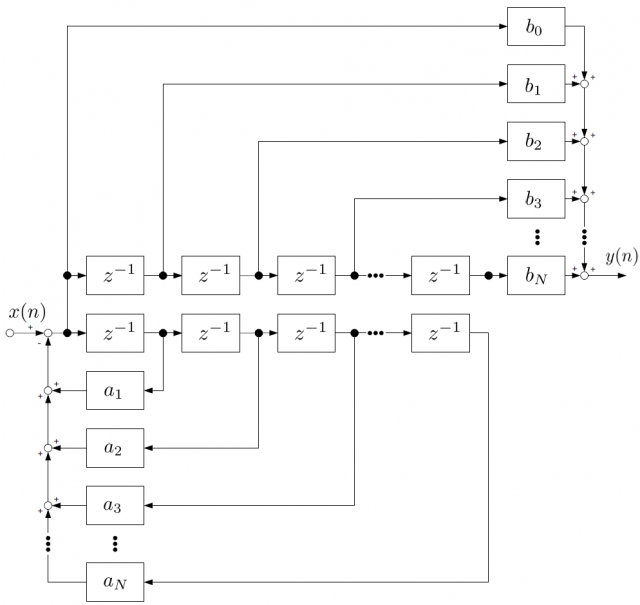
下半分についても、フィードバックの加え合わせ点を除けばFIRフィルタと同じです。FIRフィルタと同じ形の部分についてまず伝達関数を計算してみると次のように書き換えられます。
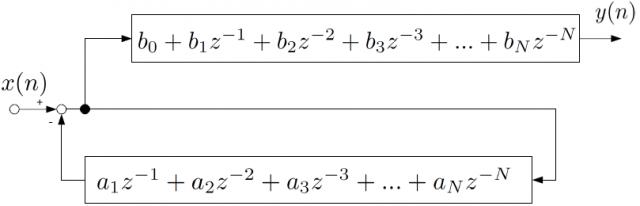
整理するとこうなります。

このような形にすればフィードバック部分についても容易に計算できますね。

以上から、このIIRフィルタの伝達関数は次式になります。
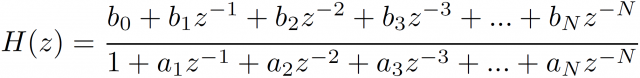
きれいな有理式になりました。伝達関数上の係数がそのままブロック線図の係数に対応していることがわかります。実現したい伝達関数が決まっていれば、フィルタの係数を決めることができるわけです。
ディジタルフィルタを構成する3大要素
FIRフィルタとIIRフィルタのブロック線図を見て分かる通り、ディジタルフィルタは次の3つの要素で構成されています。
- 遅延素子
- 係数
- 加算器
案外アナログっぽい感じがしないでしょうか。
アナログコンピュータの場合
伝達関数をベースにディジタルフィルタをプログラムする方法を考えてみましたが、アナログコンピュータにアナログフィルタをプログラムする方法についても同様に考えてみます。何かのヒントになるかもしれません。
直接型IIと同じ形をアナログで考える
ディジタルフィルタの場合、直接型IIという形は伝達関数を決めれば直接係数に反映でき、それを実現できることがわかりました。ところでこの形のzをsに置き換えてみたらどうでしょうか。s^-1という表現は習慣上あまり使われないので1/sと表現します。また、分母分子のべき表現もアナログの習慣に合わせて少し変形します。
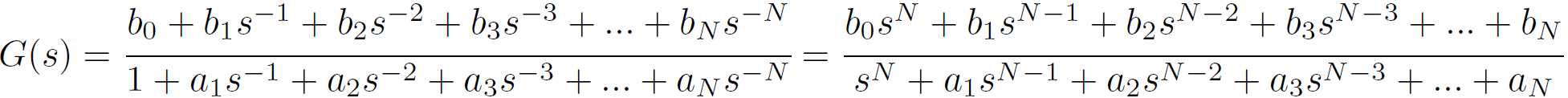
z^-1は遅延素子を表していましたが、1/sは積分器を表しています。アナログフィルタもディジタルフィルタと同じように、伝達関数が決まっていればこの形にすることで実現が可能なことがわかります。
以上のことからあくまでブロック線図上での話になりますが、アナログフィルタを構成する3大要素は次の3つであるといえます。
- 積分器
- 係数
- 加算器
これがアナログコンピュータでフィルタをプログラムするときに使われた手法です。アナログでもディジタルでもコンピュータ上では似通った手法でプログラムされていたわけです。
回路上にアナログフィルタを作成するときは積分器そのものを使うのではなくコイルやコンデンサが使われることが多いですが、実際にこの実現方法を使った有名な回路もあります。それが状態変数型フィルタです。
アナログフィルタもディジタルフィルタも案外地続きな技術のように思えてこないでしょうか。
アナログフィルタとディジタルフィルタの相違点
ここまでで見えてくるのが、アナログフィルタとディジタルフィルタの相違点です。
それぞれの3大要素で違いがあるのは、ディジタルは遅延素子、アナログは積分器という部分ですね。
RCフィルタの伝達関数
アナログコンピュータにフィルタをプログラムする際はディジタルフィルタと同じような手法が使われることを解説しました。しかし、回路の素子として積分器そのものはありませんから、よくある電気回路による実現の観点からも考えてみます。
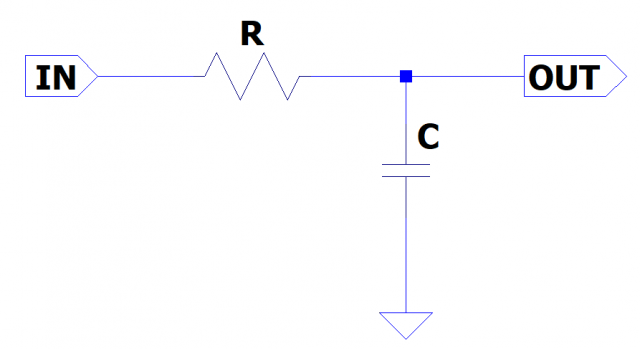
この回路の出力電圧はオームの法則から、Cに流れる電流とCのインピーダンスの積になります。Cのインピーダンスは周波数領域で考えて1/jωCと書く場合が多いですが、ラプラス変換されたインピーダンスを考えて1/sCとすることもできます。これを使うと
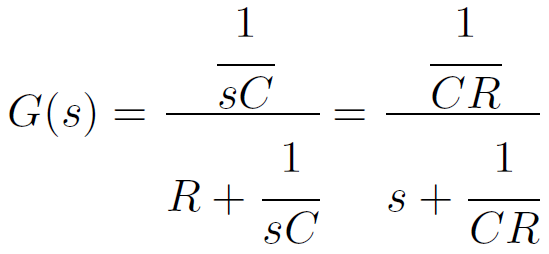
という伝達関数が求まります。
この伝達関数を積分器を使って表現すれば、次のようになります。
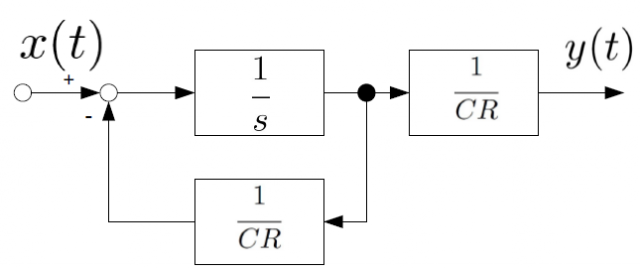
アナログコンピュータにRCフィルタをプログラムするなら、このようにするわけですね。
この積分器の部分を何らかの方法を使ってディジタルの世界へ持ち込めれば、RCフィルタをディジタルフィルタとして実装できそうです。
念の為、LTspiceでRCによる回路と、伝達関数表現、積分器による表現それぞれの結果の一致を確かめてみます。
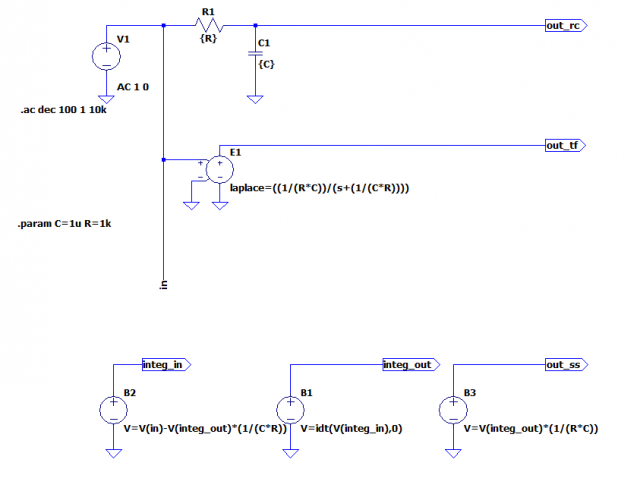
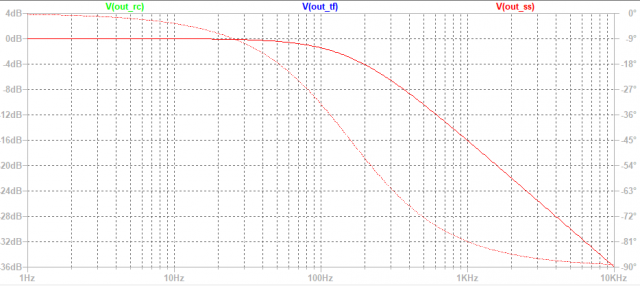
積分器をどうやってディジタルの世界に持ち込むか
遅延素子を使って積分器の動きをシミュレートできればよいわけです。その方法を考えていきます。
ディジタルの世界での積分は足し込み
変数を一つ用意してそこに入力値を足し込んでいけば積分器が作れそうです。
まずは試してみる
Xcosを使ってシミュレーション
Scilabという数値計算ソフト(フリーソフト)に付属しているXcosというツールを使うと、ブロック線図を入力するだけでシミュレーションが可能です。
遅延素子を次のように接続すると、前回の出力に今回の入力を足して出力するという動きを1サンプルごとに繰り返します。結果として入力値を積算する動きになります。
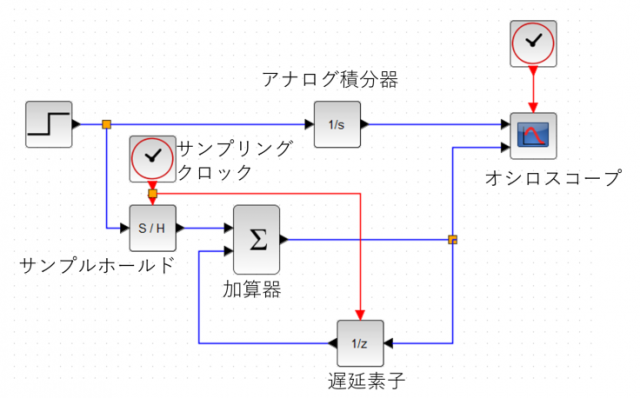
サンプリング周波数は、10 [Hz]とします。赤い時計のブロックが、この周波数を作ります。
比較のために、アナログの積分器も配置します。
入力としては、単位ステップ関数を考えます。
シミュレーション結果
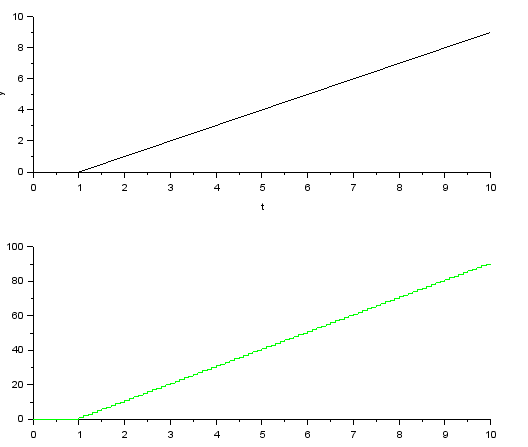
上がアナログの積分器の出力、下が今回考えたディジタルでの積分器の出力になります。
出力のスケールが大きく変わってしまいました。サンプリング周波数が高ければ高いほど、足し算を行う回数も増えるのでこの影響を考慮しないとなりません。
入力にサンプリング周波数の逆数=サンプリング時間を掛け算してシミュレーションしてみます。
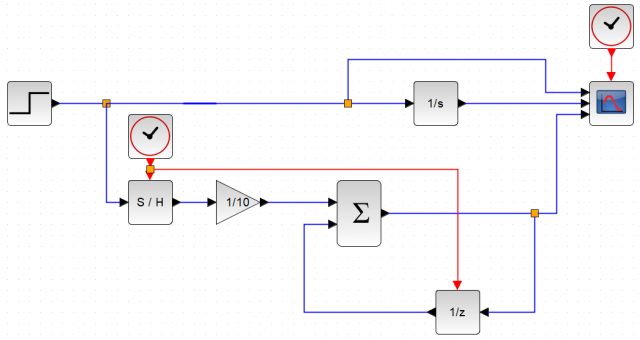
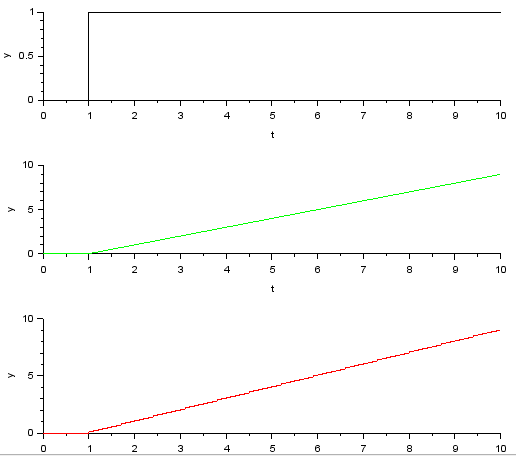
今度は同じスケールになりました。これがディジタルの積分器です。
ディジタル積分器のバリエーション
いくつかの実現方法が考えられます。
後退オイラー法(後退差分法)
さきほど試した方法です。改めてブロック線図を書くと、次のようになります。Tはサンプリング時間を意味します。
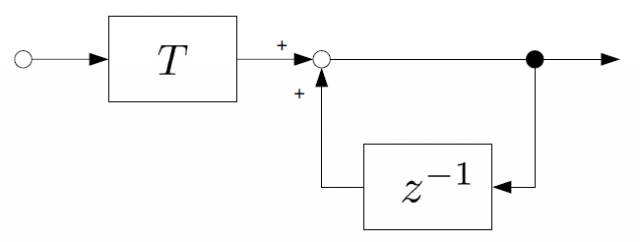
伝達関数は、ブロック線図から次のように求められますね。
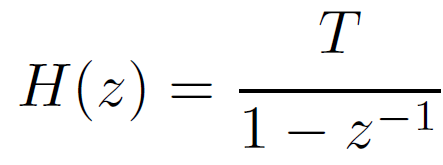
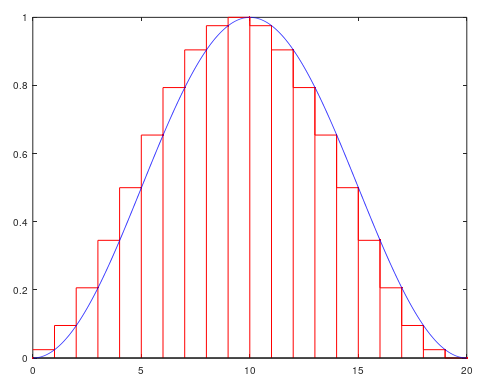
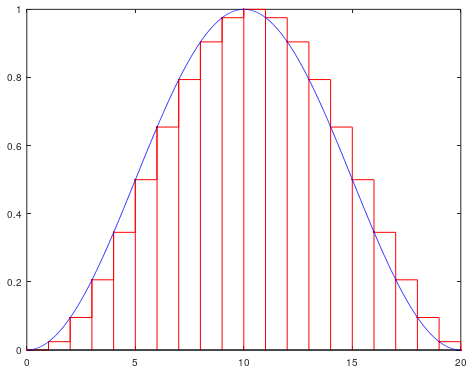
これは積分を長方形の面積の和として近似していることになります。
前進オイラー法(前進差分法)
遅延素子の位置が後退オイラー法とは違います。後退オイラー法に対して、1サンプル遅れた結果を出力します。
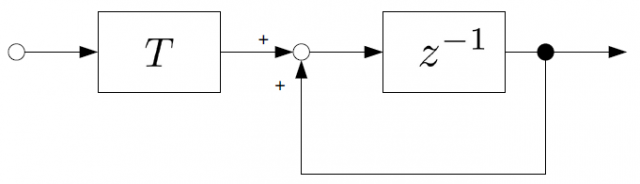
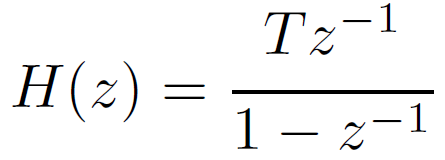
こちらも積分を長方形の面積の和として考えるものです。
後退オイラー法と前進オイラー法の比較
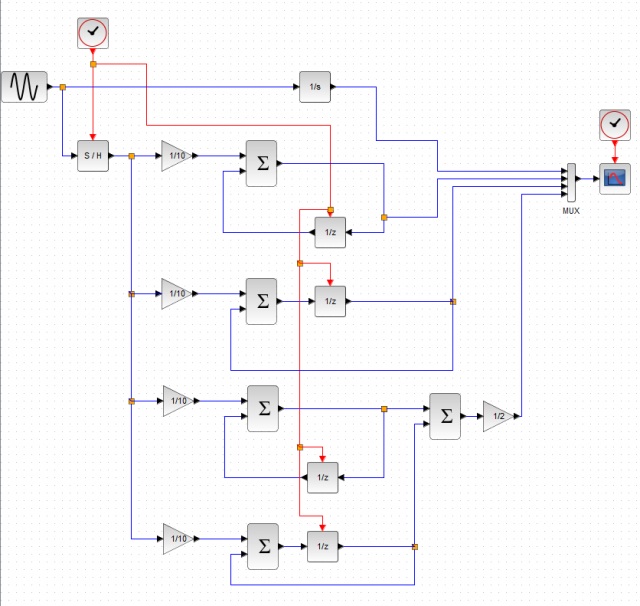
またXcosでシミュレーションしてみましょう。今度は入力波形として正弦波を考えてみます。
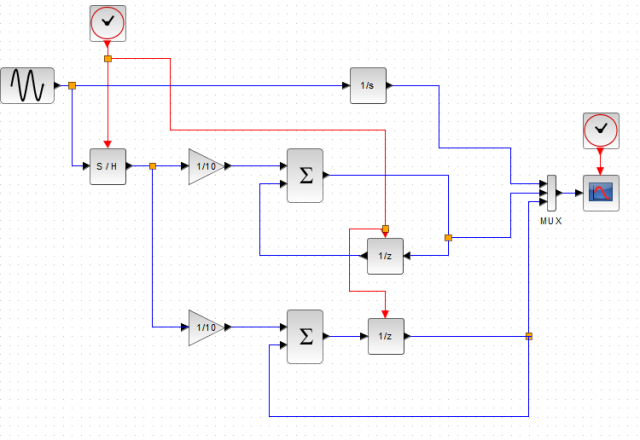
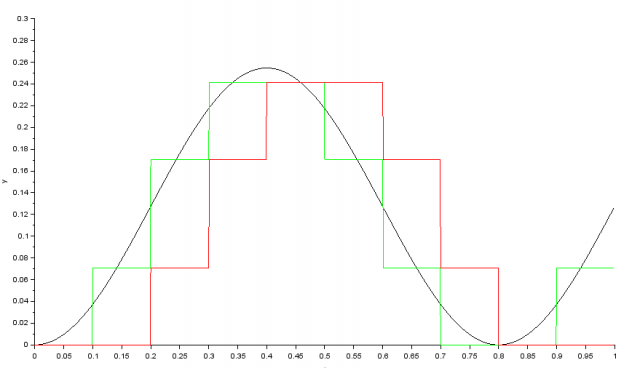
黒がアナログ積分器、緑が後退オイラー法、赤が前進オイラー法の結果です。後退オイラー法ではアナログで積分した場合に対して位相が進み。前進オイラー法では位相が遅れるという結果になりました。
位相の遅れや進みが不都合な場合もあるので、この2つの中間を考えた、次のような方法も知られています。
双一次変換(台形差分法)
後退オイラー法と前進オイラー法の平均値を取った、双一次変換と呼ばれる方法です。ブロック線図と伝達関数を示します。ブロック線図がやや冗長ですが、前述の2つの平均値であるという点に着目した表現にしています。
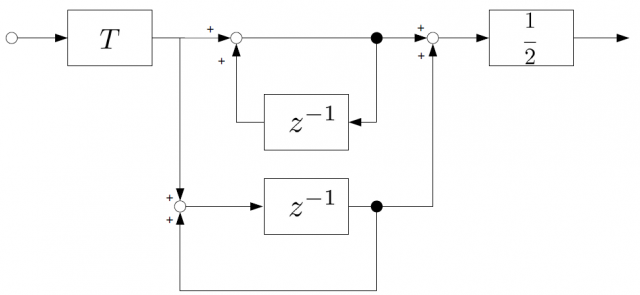
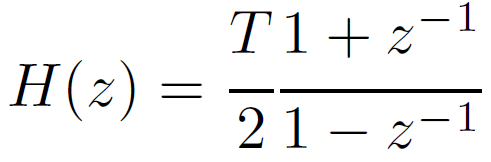
後退オイラー法と前進オイラー法との違いは、積分を長方形ではなく台形の面積の和として近似している点です。
双一次変換も含めて比較
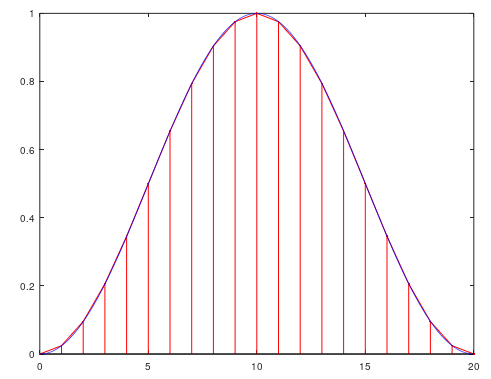
後退オイラー法、前進オイラー法、双一次変換を比較してみます。
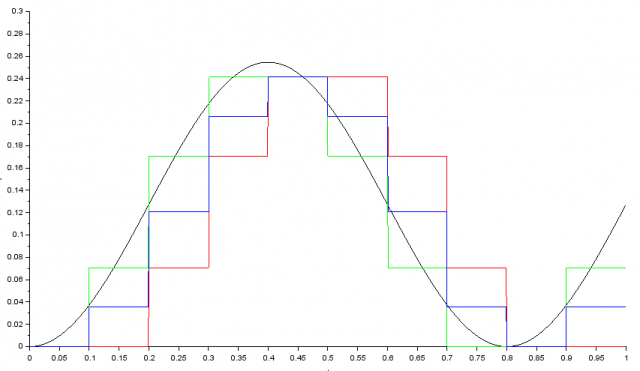
サンプリング点で考えると、青いプロットの双一次変換が最も誤差が小さいことがわかります。
では、どれを使うのか
3つの方法を紹介しましたが、実際どれを使えばよいでしょうか。扱う信号に対してサンプリング周波数が十分に高ければ、どれを使っても問題ない場合が多いです。実装上の都合で選ぶとよいでしょう。パワエレ分野などでは後退オイラー法が使われることが多いようです。
信号処理や制御の分野で双一次変換が好まれる理由の一つとしては、アナログ←→ディジタルどちら方向の変換でも必ず安定性が保存されるという点があります。
sとzの関係を考える
積分器の伝達関数は1/sなので、ディジタルで積分器を実現する3通りの方法の伝達関数からそれぞれsとzの関係を次のように考えたことになります。
後退オイラー法
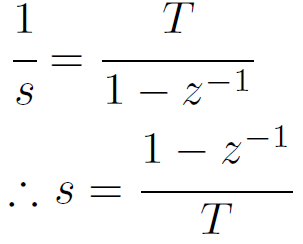
前進オイラー法
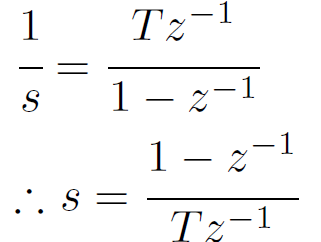
双一次変換
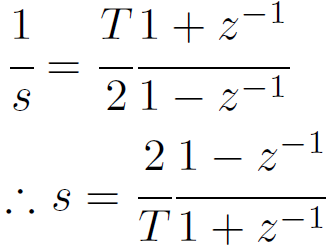
このようにsとzの関係性が明らかになったので、アナログフィルタの伝達関数のsを単純にこれらに置き換えることでディジタルフィルタの伝達関数に変換することが可能になります。
別の角度からの見方
さて、積分器を直感的な考え方で遅延素子により構成し、sとzの関係を導くことができましたが、z変換の定義から本来次の関係があります。
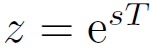
z^-1と同じ働きをする要素をラプラス変換で表現すればむだ時間要素となることからもこの関係がわかります。
指数関数のマクローリン展開を考えることで以下の関係を導くことが可能です。
前進オイラー法
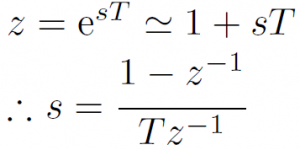
後退オイラー法
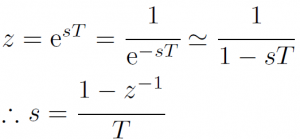
双一次変換
分母と分子の次数が一致するといろいろと都合が良いということで、次のように変形してから展開します。分母分子をそれぞれ一次で近似するので、双一次変換と呼ばれます。
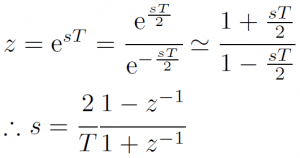
実際に設計
上の方で取り上げたRCフィルタについて、これをディジタルフィルタとして実現してみようと思います。
伝達関数を求める
RCフィルタの伝達関数を再掲します。これのsをzで表せばよいわけです。
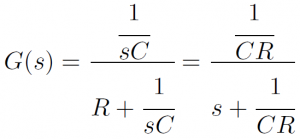
後退差分法によりsをzに変換すると次の伝達関数が得られます。
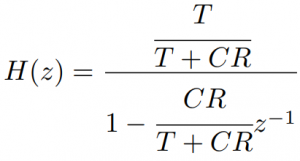
この式から、直接型IIとして実装する場合の係数は次のようになります。
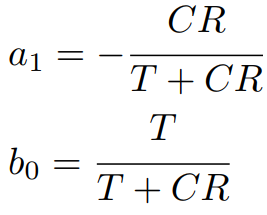
ブロック線図は次のようになります。
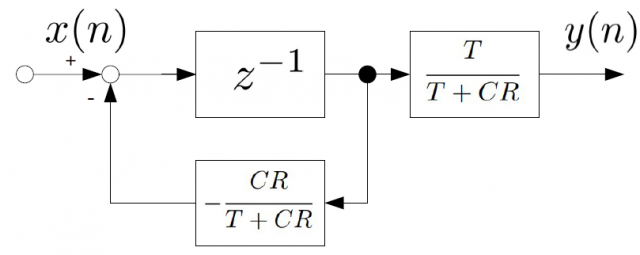
Xcosでシミュレーション
直接伝達関数を入力し、シミュレーションできます。サンプリング時間は1/48e3としました(サンプリング周波数48kHz)。Xcosで周波数特性を確認するのは少し面倒なので、ステップ応答をアナログフィルタと比較してみます。
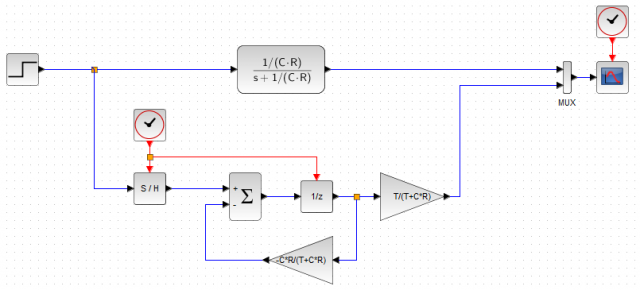
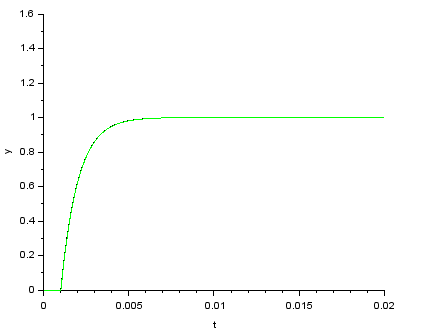
このように、結果がほぼ一致しました。アナログフィルタをうまくディジタルの世界に持ち込めたことになります。
実装時は、このブロック線図のとおりにプログラムすればよいわけです。
Octaveでもシミュレーション
さて、ブロック線図をそのまま扱える点でXcosは素晴らしいのですが、使い勝手があまり良くないので私は好きではありません。前回の記事で使ったOctaveで試してみます。
伝達関数が決まっているので、filter関数を使って簡単にシミュレーションできます。
伝達関数の分子、分母それぞれの係数を次数が高い方から順に(0次の項が最初)ベクトルとして入力します。
filter( [b0 b1 b2], [a0 a1 a2], in )
といった要領です。
今回の場合、次のようになります。
C = 1e-6;
R = 1e3;
T = 1/48e3;
b0 = T/(T+C*R);
a1 = -C*R/(T+C*R);
filter([b0], [1 a1], audio);前回同様に猫の鳴き声に適用してみます。
C = 1e-6;
R = 1e3;
T = 1/48e3;
b0 = T/(T+C*R);
a1 = -C*R/(T+C*R);
[audio, fs_audio] = audioread("VSQSE_965_cat_6.wav"); %入力音声の読み込み
audio = resample(audio, 48e3, fs_audio); %入力音声のサンプリング周波数を48kHzに変換
audio = audio(:,1); %片chのみ抽出
audio = [audio;zeros(fs_audio*1,1)]; %入力音声の末尾に1秒の無音を付加
filter_out = filter([b0], [1 a1], audio); %フィルタ処理
filter_out = filter_out / max(abs(filter_out)); %最大値が1になるよう正規化
soundsc(filter_out, fs_audio, 16)
audiowrite("cat_rc_lpf.wav",filter_out, fs_audio);高音がこもった感じになりましたね。RCフィルタと同じ効果が得られました。
IIRフィルタは速い
FIRフィルタとIIRフィルタの使い分けの一つとして、多くの場合IIRフィルタの方が少ない遅延素子で実現でき、処理速度が速くなります。
リアルタイム処理に堪えるリバーブエフェクタ
前回の記事で、FIRフィルタを使って音声にリバーブ効果をかける例を示しました。実際に実行してみるとわかるのですが、非常に長い処理時間がかかります。リアルタイムでの実行はちょっと厳しそうです。
カラオケなどではリアルタイムに気持ちの良いリバーブがかかりますが、おそらくIIRフィルタを使って実現しているのではないかと思います。
IIRフィルタの応用“シュレーダー・リバーブ”
IIRフィルタを応用したリバーブとして、シュレーダー・リバーブと呼ばれるアルゴリズムが有名なようです。こちらのサイトを参考に、ブロック線図として書き直すと以下のようになります。
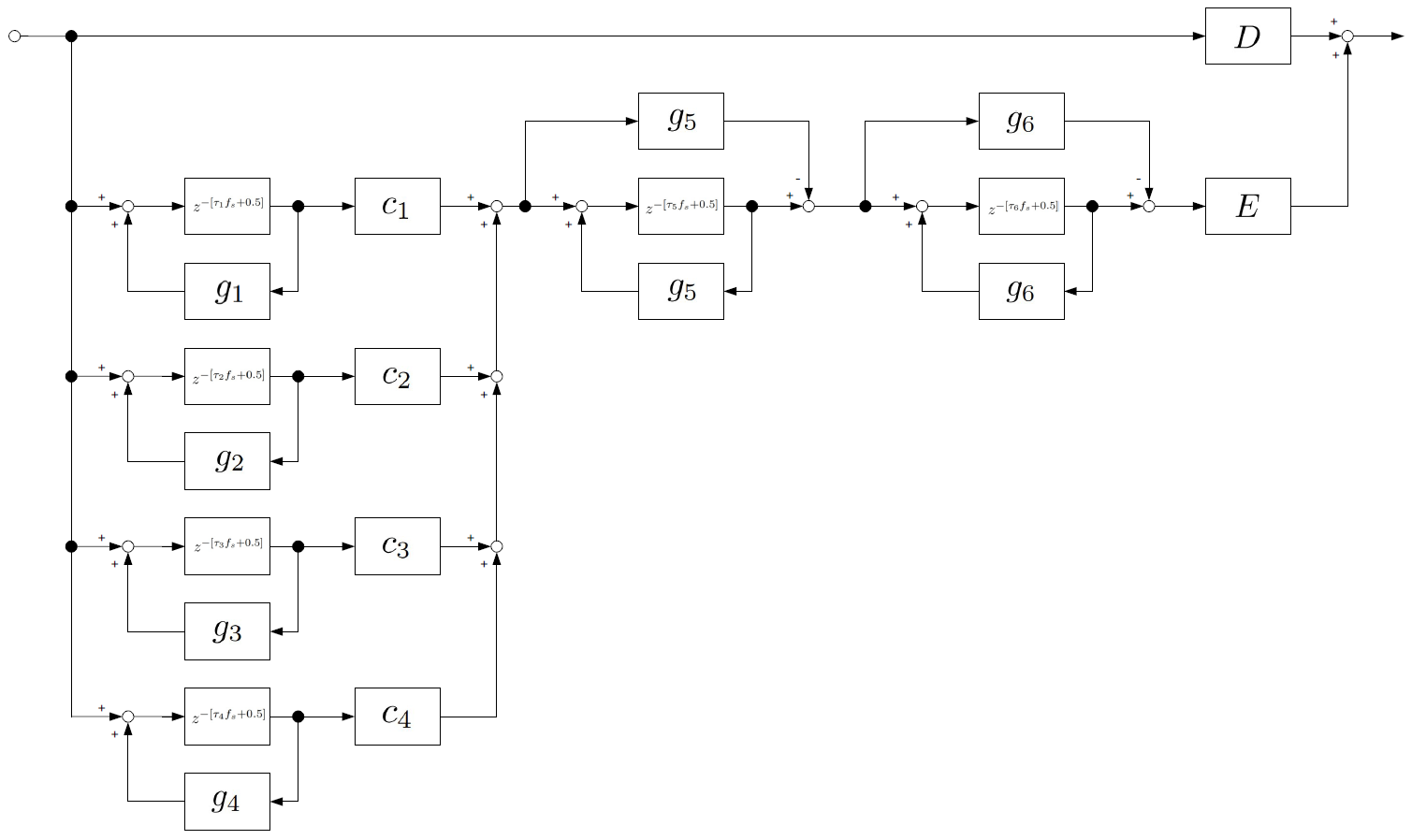
このブロック線図から伝達関数を計算し、Octave上で動くようにしたのが次のスクリプトです。パラメータはすべて参考サイトそのままですが、DとEのゲインについて記載がなかったので、仮にD=1,E=0.3としました。
fs = 48e3;
% オーディオデータの読み込み %
[audio_in, fs_audio] = audioread("VSQSE_965_cat_6.wav");
% 片chのみ抽出 %
audio = audio_in(:,1);
% サンプリングレートを48kHzに変換、末尾に2秒の無音を付加 %
audio = [resample(audio,48e3,fs_audio);zeros(2*48e3,1) ];
% パラメータ(遅延時間) %
tau1 = 39.85e-3;
tau2 = 36.10e-3;
tau3 = 33.27e-3;
tau4 = 30.15e-3;
tau5 = 5.0e-3;
tau6 = 1.7e-3;
% 遅延サンプル数 %
delay_sample_c1 = round(tau1*48e3);
delay_sample_c2 = round(tau2*48e3);
delay_sample_c3 = round(tau3*48e3);
delay_sample_c4 = round(tau4*48e3);
delay_sample_a1 = round(tau5*48e3);
delay_sample_a2 = round(tau6*48e3);
% パラメータ(フィードバックゲイン) %
g1 = 0.871402;
g2 = 0.882762;
g3 = 0.891443;
g4 = 0.901117;
g5 = 0.7;
g6 = 0.7;
%パラメータ(直接音と残響音のゲイン)%
D = 1;
E = 0.3;
% 伝達関数(コムフィルタ)r %
b_c1 = [zeros( 1,delay_sample_c1 ) 1];
a_c1 = [1 zeros(1,delay_sample_c1 - 1) -g1];
b_c2 = [zeros( 1,delay_sample_c2 ) 1];
a_c2 = [1 zeros(1,delay_sample_c2 - 1) -g2];
b_c3 = [zeros( 1,delay_sample_c3 ) 1];
a_c3 = [1 zeros(1,delay_sample_c3 - 1) -g3];
b_c4 = [zeros( 1,delay_sample_c4 ) 1];
a_c4 = [1 zeros(1,delay_sample_c4 - 1) -g4];
% 伝達関数(オールパスフィルタ) %
b_a1 = [-g5 zeros( 1,delay_sample_a1 - 1 ) 1];
a_a1 = [1 zeros(1,delay_sample_a1 - 1) -g5];
b_a2 = [-g6 zeros( 1,delay_sample_a2 - 1 ) 1];
a_a2 = [1 zeros(1,delay_sample_a2 - 1) -g6];
% コムフィルタ(C1~C4)の出力を演算 %
c1 = filter( b_c1, a_c1, audio );
c2 = filter( b_c2, a_c2, audio );
c3 = filter( b_c3, a_c3, audio );
c4 = filter( b_c4, a_c4, audio );
% オールパスフィルタ(a1~a2)の出力を演算 %
a1 = filter( b_a1, a_a1, c1 + c2 + c3 + c4 );
a2 = filter( b_a2, a_a2, a1 );
soundsc( E*a2 + D*audio, 48e3, 16);
audiowrite("cat_schroeder_reverb.wav",E*a2 + D*audio, fs_audio);
こちらも猫の鳴き声に適用してみますが、処理は一瞬で終わります。
このように、処理速度が求められる場合にIIRフィルタが適しています。
【おまけ】LTspiceでディジタルフィルタをシミュレーションする
回路シミュレータのLTspiceですが、サンプルホールド機能や伝送路モデルによる遅延などが利用できるため、工夫するとディジタルフィルタのシミュレーションを行うことができます。
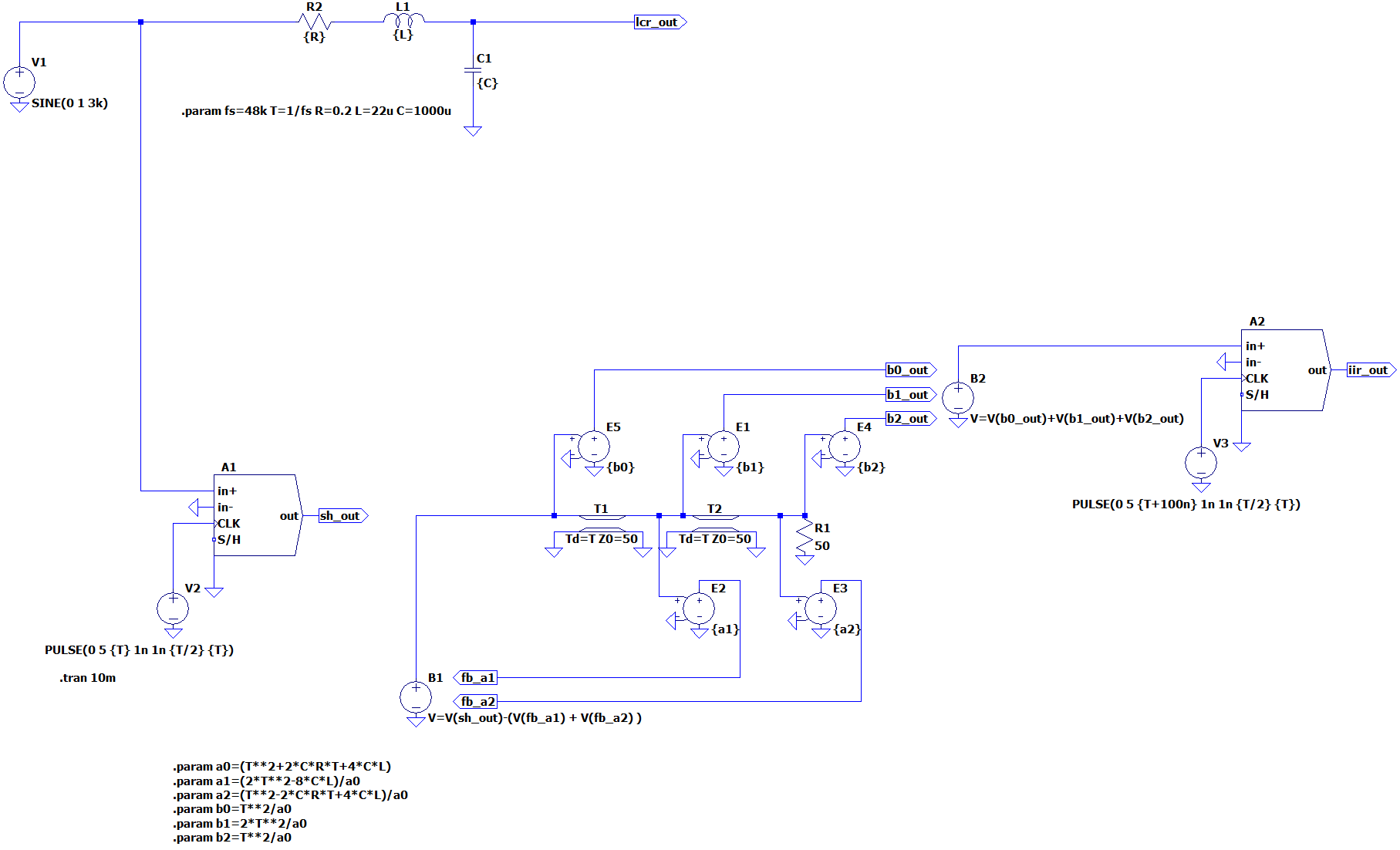
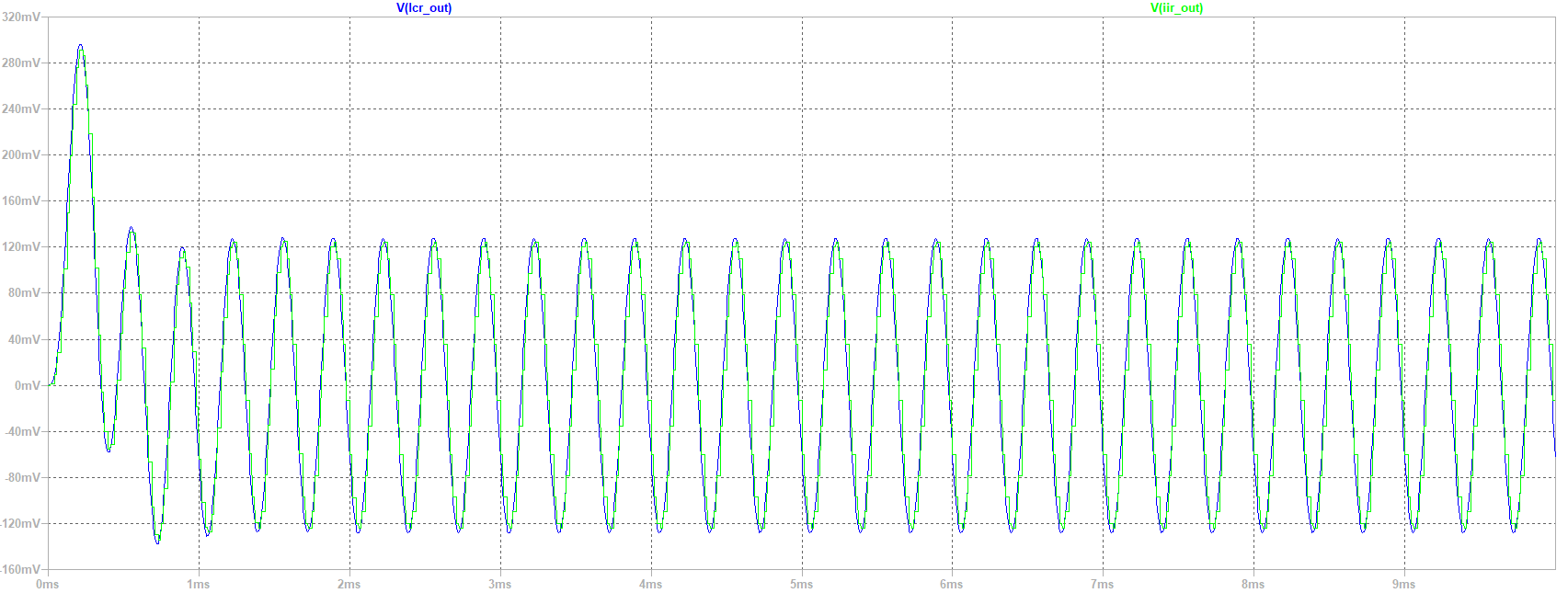
あくまでアナログ回路のシミュレータですのでディジタルフィルタの検証を行う用途ではお勧めできませんが、アナログ回路と並べて結果を比較するとなかなか楽しいものです。以下は、LCRフィルタとそれを双一次変換により直接型IIで実現したIIRフィルタを同時にシミュレーションするものです。
L,C,Rのいずれを変更してもディジタルフィルタに反映されます。
LCRフィルタの伝達関数および双一次変換によって得たディジタルフィルタの伝達関数は次式となります。
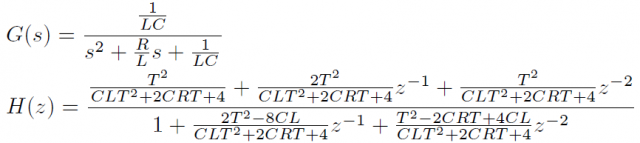
IIRフィルタを実装するとき注意すること
固定小数点での実装は茨の道
FIRフィルタの場合は内部の数値のダイナミックレンジを事前に知ることが簡単なので固定小数点でも実装しやすいのですが、IIRフィルタの場合固定小数点での実装は茨の道です。形を変更する必要が出てくることもあります。トラブルを避ける意味では、実行環境が許す限り浮動小数点を使うのが無難です。
高い次数を直接実装しない
直接型IIという実現方法を紹介しました。これは原理的には次数がいくつでも実現できます。しかし、3次以上になると各係数が極端に違う値となり、演算誤差などが問題になってきます。高い次数の場合、伝達関数を因数分解することで2次の伝達関数の縦続接続に変換してから実装します。
安定性に注意する
本記事で説明した設計手法においては問題になることは少ないですが、フィードバック系ですので発振、発散というトラブルがつきものです。この点もアナログ回路と似ていますね。
おわりに
アナログフィルタの積分要素に着目し、ディジタルフィルタに変換する方法について解説しました。
簡単な記事にしたかったので、双一次変換を入れるかどうか迷いました。オイラー法だけにした方が全体的にシンプルな記事になったかもしれません。
高専1年の時先輩に「ディジタルフィルタに興味があります」と言ったとき、次のようなアドバイスを頂きました。
- ディジタルの世界では微分は差分、積分は足し込みになる
- 双一次変換というやつを使うとディジタル化できるらしいが、俺にはこれが全くわからない。とりあえず式はこれ。
とても良いアドバイスだったと思います。しかし積分を足し込みで実現するところまで理解がたどり着いているのに双一次変換が全くわからないとのことで、ある意味これが初学者への障壁になっているのではないかと今考えると思います。
確かに、連続系の離散化には双一次変換を使う、これはz変換の定義のパデ近似であると形式的な流れで説明されても理解が追いつきにくい部分があります。
双一次変換も台形則を使った積分の近似と考えれば積分が足し込みであるという理解からほんの一歩先にあるものなので、そこで躓く場合があるのはもったいないと思いあえて今回の記事に入れてみました。
入門書を読むための入門資料のような感じでお役に立てれば幸いです。
参考文献
- 谷萩 隆嗣, ディジタル信号処理と基礎理論, コロナ社, 1996
- 谷萩 隆嗣, ディジタルフィルタと信号処理, コロナ社, 2001
- 三谷 政昭, 今日から使えるラプラス変換・z変換, 講談社, 2011
- 尾知 博, シミュレーションで学ぶディジタル信号処理, CQ出版, 2007
- 三浦武雄, アナログ電子計算機のソフトウエア, コロナ社, 1967
- ドナルド・G. シュルツ, ジェームズ・L. メルサ ( 久村富持訳), 状態関数と線形制御系, 学献社, 1970
- 酒井 幸市, 高専学生のためのディジタル信号処理, コロナ社, 1996
- 河村 篤男, 現代パワーエレクトロニクス, 数理工学社 , 2005
- 辻 峰男, ディジタル制御システム, 長崎大学学術研究成果リポジトリ, 2016
- パワエレ学生の備忘録
- パワエレと制御の技術解説
- 株式会社エー・アール・アイ
Cerevoからのお知らせ
現在Cerevoでは各種エンジニアの採用、またハードウェア共同開発・受託開発を絶賛募集しております。それぞれご関心お持ちいただける方は、以下の専用お問い合わせフォームよりご連絡お待ちしております。
- 現在募集している職種
https://cerevo.com/recruit/
- ハードウェア共同開発および受託開発のご相談
https://cerevo.com/contact/sales/
著者プロフィール
- Cerevo 電気エンジニア
最近の投稿
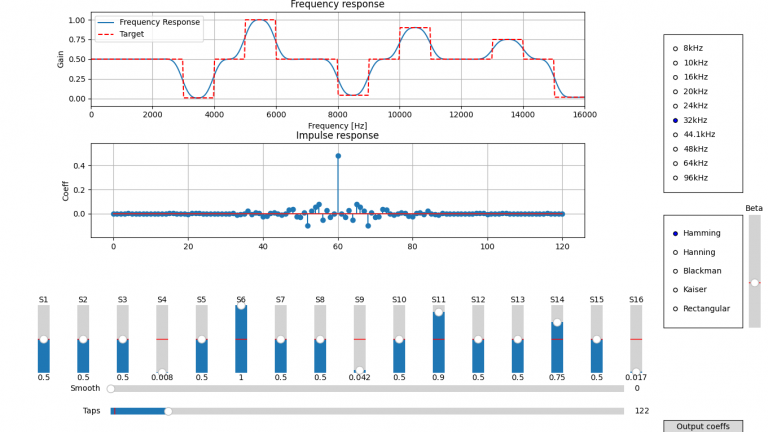 02. ソフトウェア2025.07.30インタラクティブに設計するディジタルフィルタ
02. ソフトウェア2025.07.30インタラクティブに設計するディジタルフィルタ 02. ソフトウェア2025.07.23とにかくラフに設計するディジタルフィルタ
02. ソフトウェア2025.07.23とにかくラフに設計するディジタルフィルタ 11. その他2025.07.16CP210xシリーズのCOM番号とUSBハブ上の差し込みポートを紐づける
11. その他2025.07.16CP210xシリーズのCOM番号とUSBハブ上の差し込みポートを紐づける 11. その他2025.07.09アリエク調達のアンプでアクティブプローブを作成する
11. その他2025.07.09アリエク調達のアンプでアクティブプローブを作成する