はじめに
こんにちは。電気エンジニアの早川です。
組み込みソフトや、音声を扱うソフトなどを書いているとちょっとしたフィルタを仕込みたい場面に遭遇することがあります。こういったディジタルの世界に実装するフィルタのことをディジタルフィルタと呼びますが、その理論は難解でとっつきにくい部分があります。とはいえ直感的な理解が可能な部分もあり、さらに言えばそれだけでもある程度道具として活用することは可能です。
本記事では、できるだけ直感的にディジタルフィルタを理解することを目指して解説していきます。
目次
ディジタルフィルタの種類
大きく分けて2つの種類があります。
FIRフィルタ
移動平均フィルタがこれに属します。基本的に移動平均のアルゴリズムの延長と考えることができます。今回はこちらを説明していきます。
IIRフィルタ
内部にフィードバックを持つのが特徴で、アナログ回路とよく似た原理で動作します。コイルやコンデンサのような動きをディジタルの世界で動かす、 ある意味で物理シミュレータといえるかもしれません。
FIRフィルタのアルゴリズム
FIRフィルタのアルゴリズム自体はシンプルで理解しやすいものなので、いきなりアルゴリズムの話をします。
身近なFIRフィルタ“移動平均フィルタ”
前述のように、移動平均フィルタはFIRフィルタの仲間です。Excel等でも簡単に出せますし、株価チャート等でも馴染みがありますよね。
そのアルゴリズムを図示すると次のような感じでしょう。
このような入力xを考えてみます。
これに対して長さが8の移動平均処理を行った後の出力をyとして考えてみます。
赤で囲った部分の入力にそれぞれ1/8を掛け算してそれらを足し合わせるという処理ですね。これを逐次やっていけばよいので、アニメーションで表現するとこんな感じになります。
いろいろな移動平均
Wikipediaの移動平均の項目を見ると、いろいろな種類があることがわかります。さきほどの例は8個データに対してすべて1/8を掛けてから足し合わせていました。
これは過去8個分のデータをすべて同じ重みで処理していることになります。このような移動平均を単純移動平均と呼びます。
次のような移動平均もあります。
これは加重移動平均と呼ばれ、一番新しいデータに最も大きな重みを与え、古いデータほど順次重みを小さくしていきます。こちらもアニメーションで表すと次のようになります。
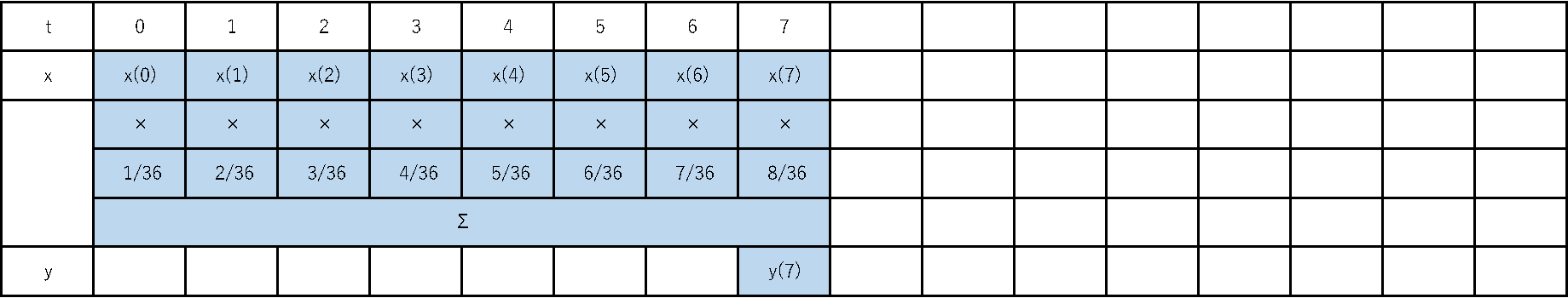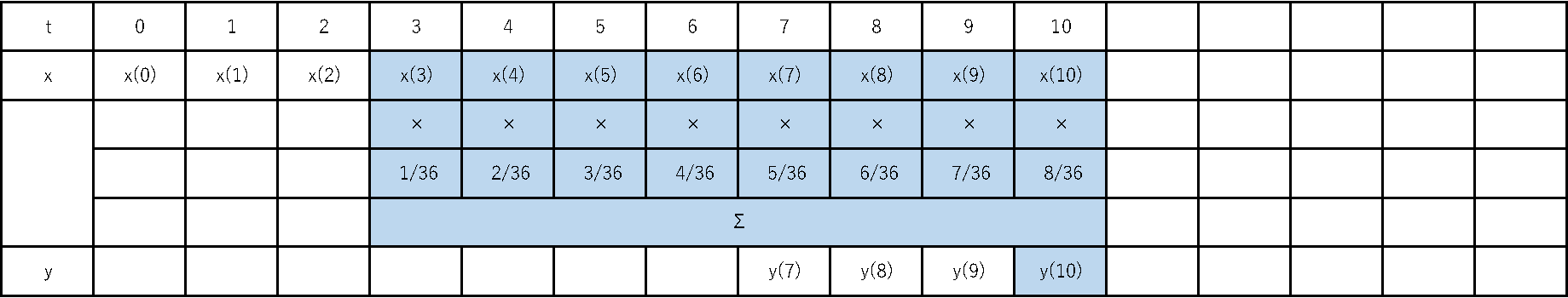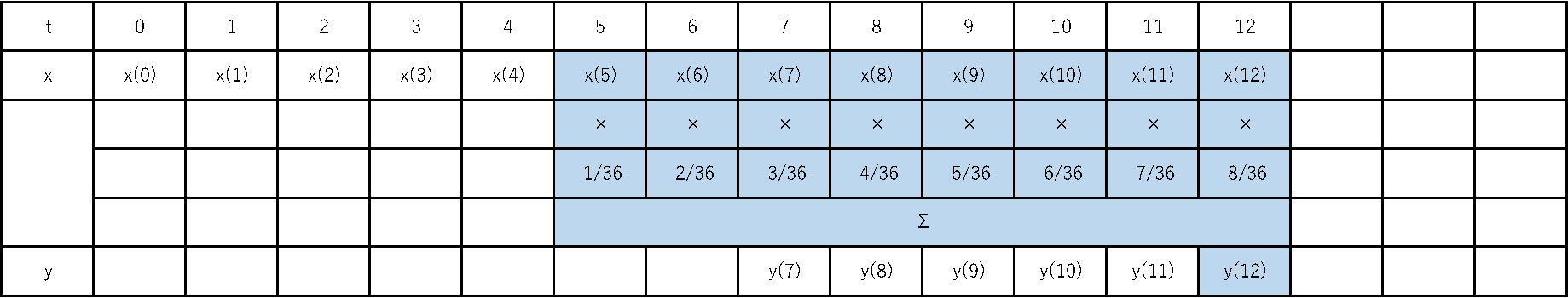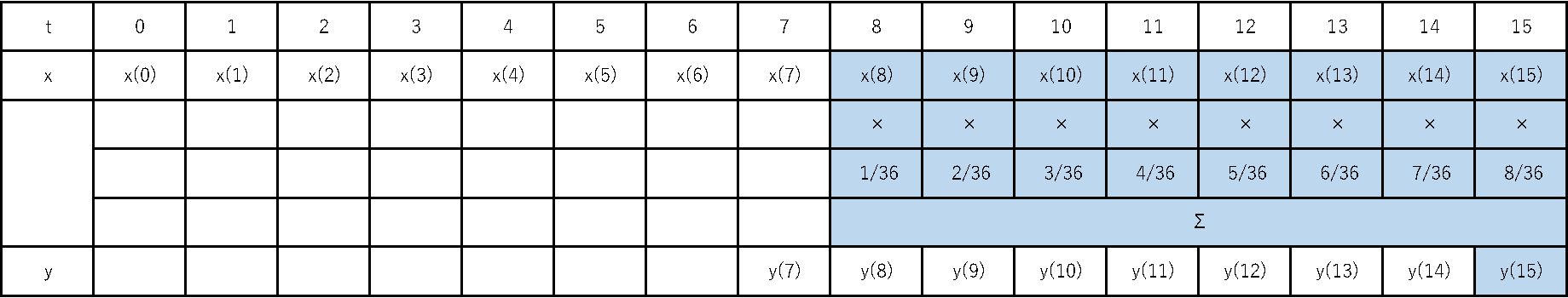
重みを一定ではなくこのように変化させることで、“新しいデータほど価値を大きく”捉えるフィルタとなります。
加重移動平均は重みを線形的に減少させますが、指数関数的に減少させる指数移動平均というのもあり、こちらのほうが一般的かもしれません。
このように重み付けをいろいろと変化させることでフィルタの特性を変化させることができます。実は、FIRフィルタの設計とはこの重みを設計することなのです。
FIRフィルタ=重み付き移動平均フィルタ
FIRフィルタと重み付き移動平均フィルタは本質的には同じものと言えます。重みをh(k) k=0,1,…,7で表せば、次のアニメーションはタップ数が8のFIRフィルタとなり、h(k)をどのようなものにするかで特性が決まります。
このように、FIRフィルタのアルゴリズム自体はシンプルなもので、実行速度にシビアな環境でなければ実装も比較的簡単です。
FIRフィルタの物理的意味
さきほどまではFIRフィルタのアルゴリズムに着目して説明しました。ここからは、少し別の角度から見ていきます。
インパルス応答とは
FIRフィルタの物理的意味を考えるため、ここでインパルス応答という概念を導入します。
馴染みのあるインパルス応答
スイカをコンコンと叩いて熟度を判断する場面を見たことがないでしょうか。他にも、コンクリートをハンマーで叩いてその時の音で異常がないか確認する打音検査なども、対象物のインパルス応答を観測していると言えます。ホールや風呂場で手を叩くと残響が聞こえますが、それがその部屋の音響的なインパルス応答と言えます。
前提条件はあるものの、インパルス応答を知ることで対象物の特性を知ることができ、様々な応用がなされています。
ディジタルの世界でのインパルス応答
ディジタルの世界で言うところのインパルス応答とは、系に単位インパルス関数を入力したときの出力です。単位インパルス関数とは、t=0のときだけ1という値を持ち、それ以外では0となる関数です。
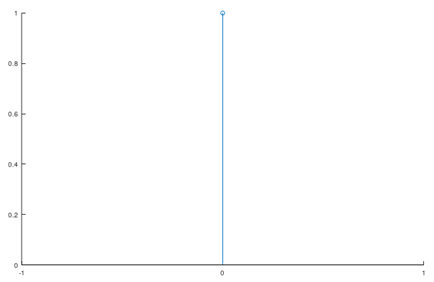
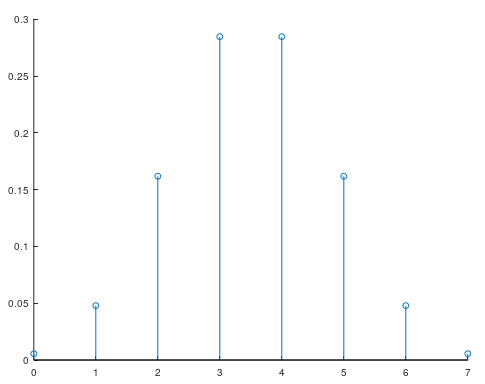
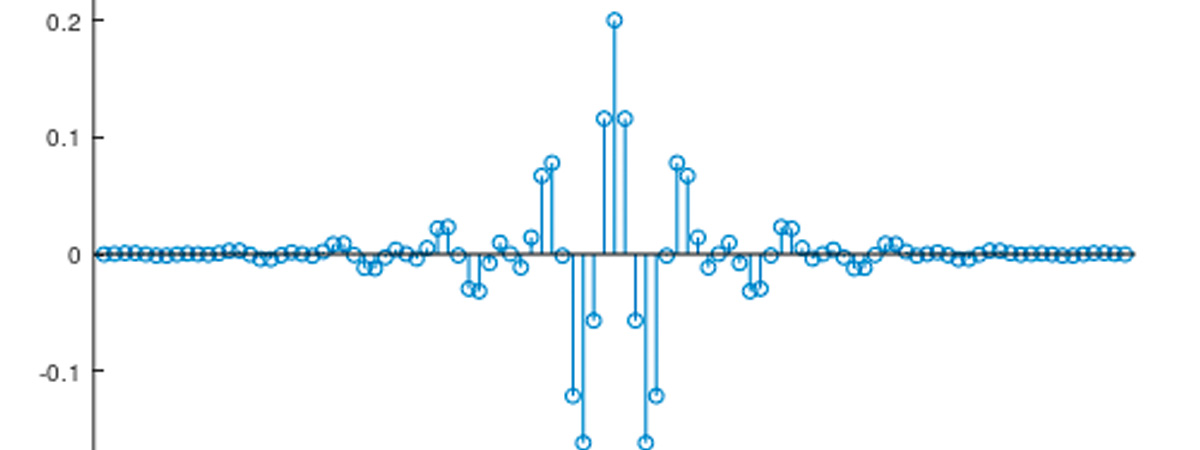
例えばFIRフィルタなどのディジタルの世界に実装された系に単位インパルス関数を入力し、こんな出力が得られたとしたらそれがその系のインパルス応答ということになります。
インパルス応答を知っていると任意の入力に対する応答を知ることができる
系のインパルス応答を知ることはその系の振る舞いのすべてを知ることです。インパルス応答を知っているとその系に対する任意の入力に対する応答を調べることができます。
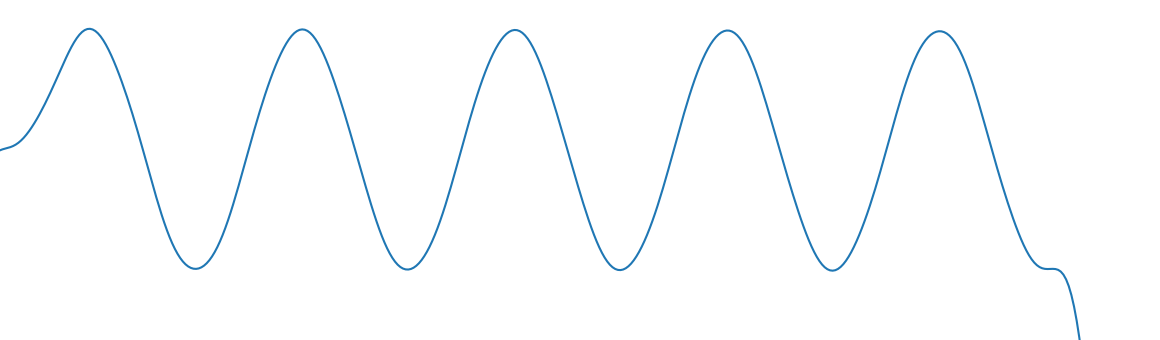
例えば、さきほどのインパルス応答を持つ系に次のような入力をしたときの応答について考えてみます。
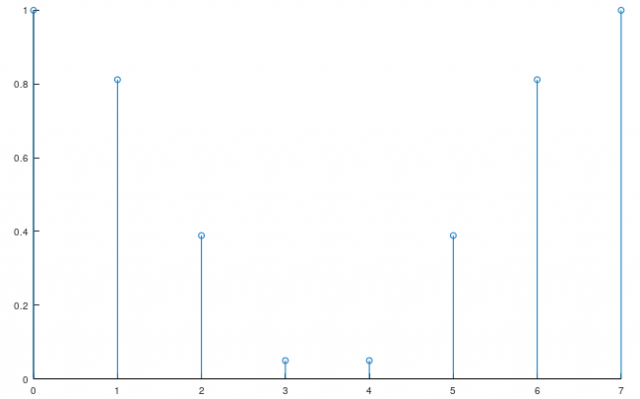
そのままでは考えるのが難しいので、入力信号をインパルス関数の重ね合わせで表現できないか考えてみます。
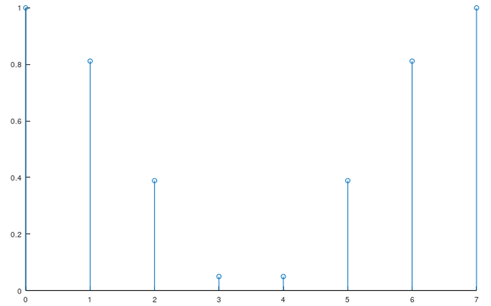
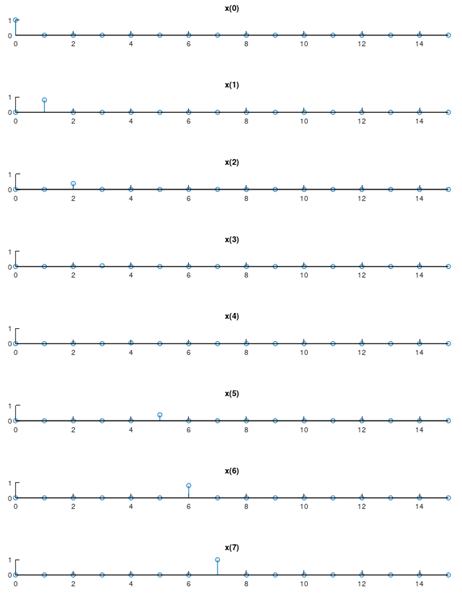
このように、複雑な入力波形も単位インパルス関数を時間的にシフトしてさらに大きさを変化させたものの重ね合わせに分解して考えることが出来ます。
この分解したそれぞれに対して応答を考えてみます。それはインパルス応答を時間シフトし、大きさを変化させたものであることがわかります。
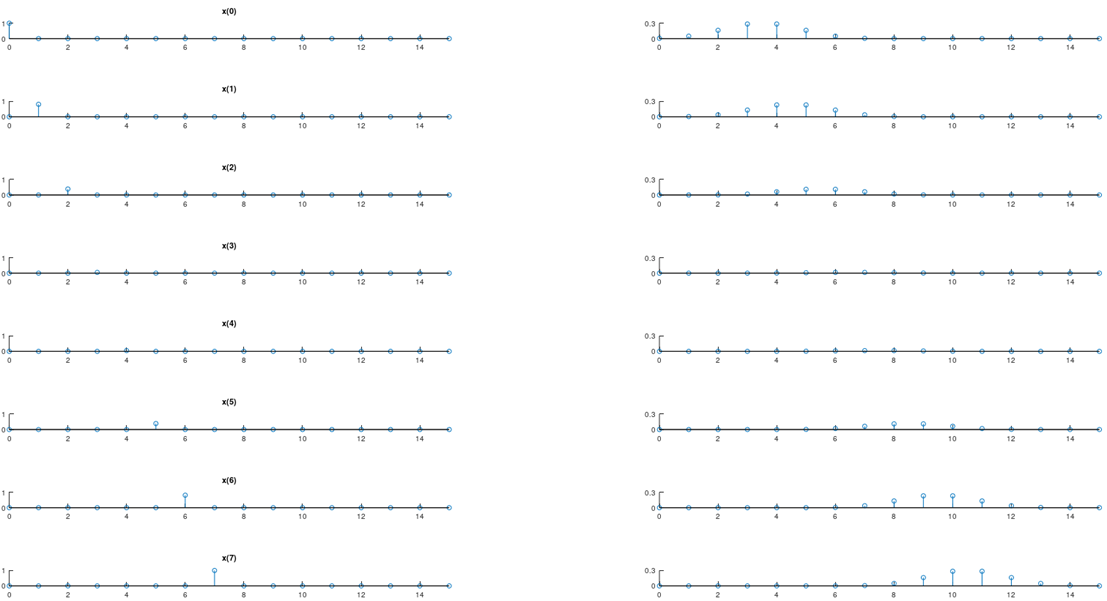
この分解して考えたそれぞれの応答を足し合わせれば、実際の応答を知ることができます。どのような信号もインパルスの重ね合わせとして捉えることができるため、それを系に入力した際の出力もその系のインパルス応答の重ね合わせになるというわけです。
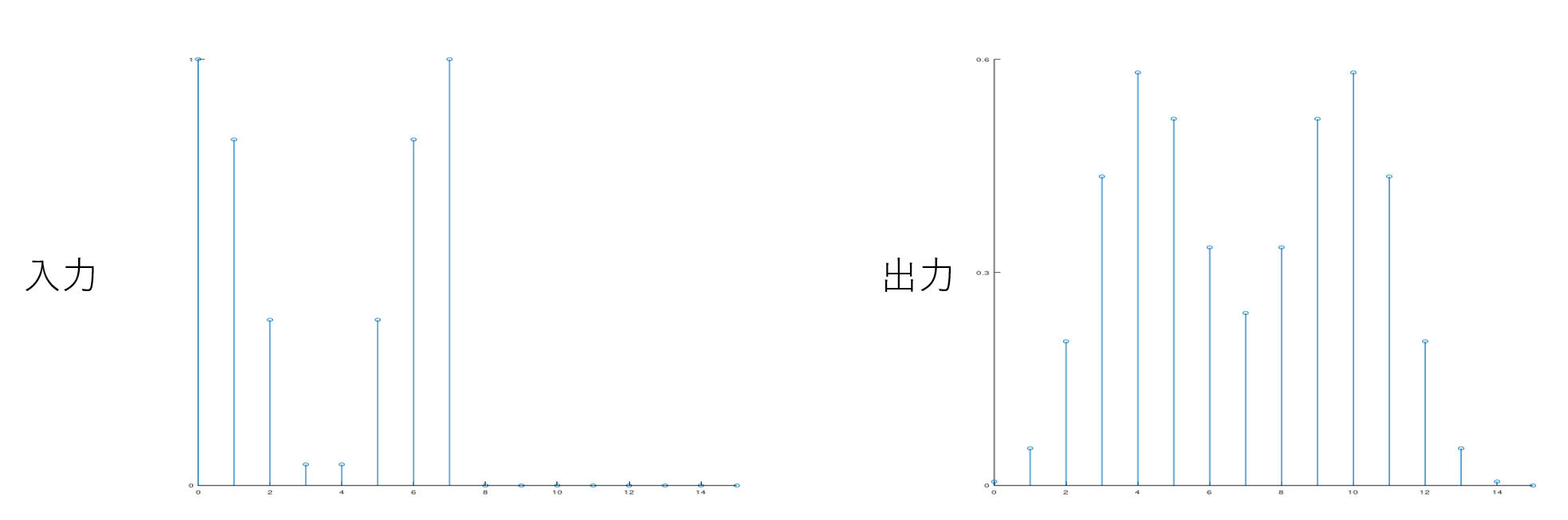
さて、インパルス応答が既知の系に任意の入力を与えたときの応答について考えてきました。
ここまでの手順が実はFIRフィルタのアルゴリズムと全く同じであったことに気が付かれたでしょうか。
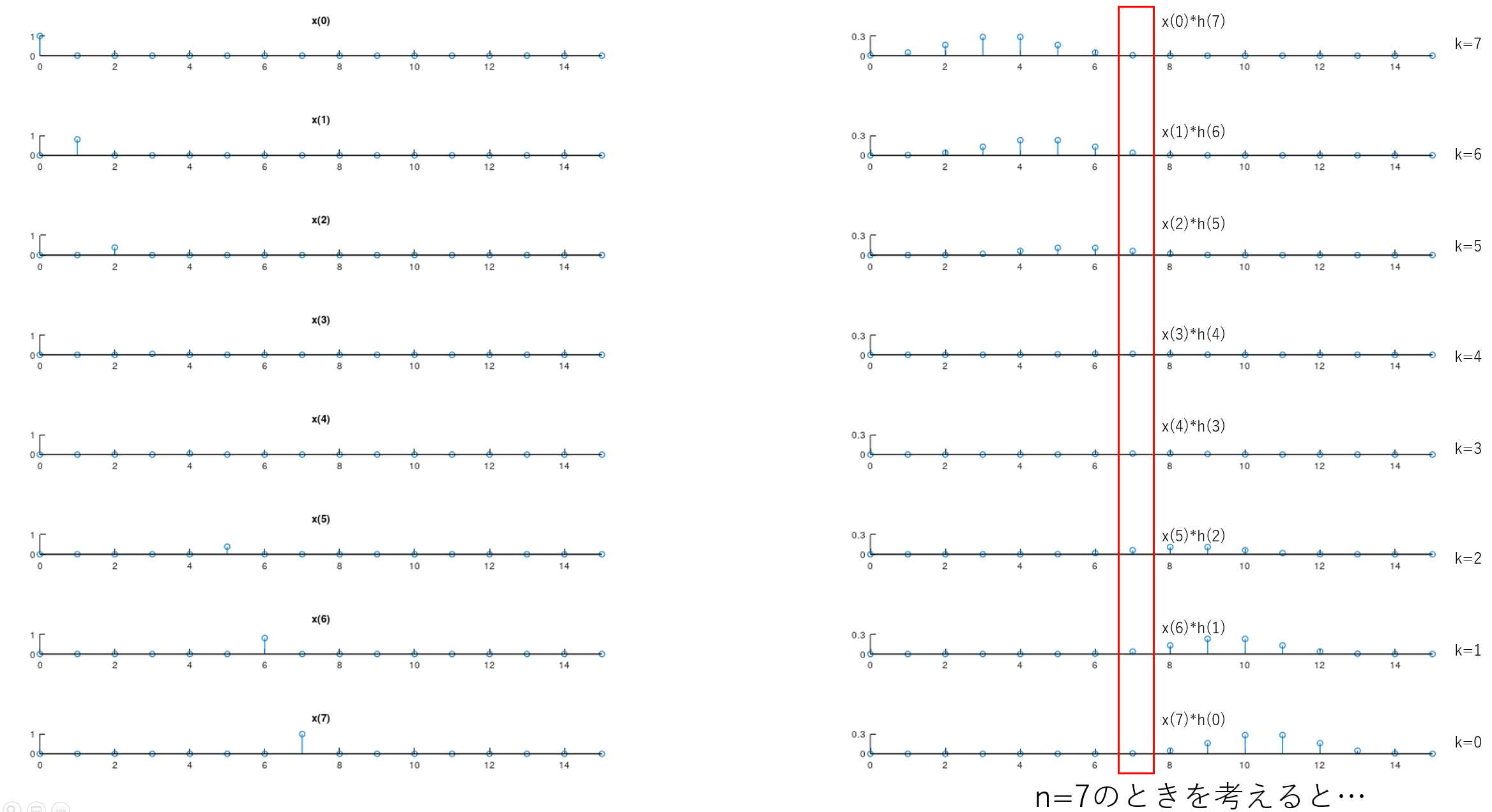
例えばn=7の場合を考えると、赤枠部分の和がy(7)になります。演算内容を追っていくと、x(7)*h(0) + x(6)*h(1) + … +x(0)*h(7)というように、移動平均として説明したFIRフィルタのアルゴリズムと全く同じであることがわかります。
これがFIRフィルタのより本質的なとらえ方になります。移動平均の重みの正体は、FIRフィルタのインパルス応答というわけです。FIRフィルタの設計=(有限長の)インパルス応答の設計ということになります。
これを定式化すると次式になります。
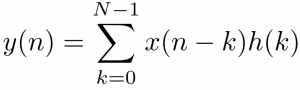
ここで、Nは有限の値でインパルス応答h(k)は有限の長さということになります。このことから、FIR( Finite Impulse Response )と呼ばれています。図示した例の場合だとNが8ですね。
この式は、ディジタルフィルタの本を開くと最初の方に書いてあります。一般的な説明だと、まずこの式から入るので直感的なイメージが難しく、とっつきにくさの原因かもしれません。数式が表しているのはさきほど説明したアルゴリズムそのものです。
インパルス応答と残響
ここまでの説明だと、まだインパルス応答という概念が仮想的なものに見えるかもしれません。身近なインパルス応答の例として、部屋の残響というものを考えてみます。
風呂場のインパルス応答
自宅の風呂場で手を叩いてそれをスマホで録音してみました。アナログの世界で理想的なインパルスを作ることはできませんが、手を叩くなどでも近似的なインパルスとして扱うことができます。これによって風呂場の残響、つまりインパルス応答を録音することができます。
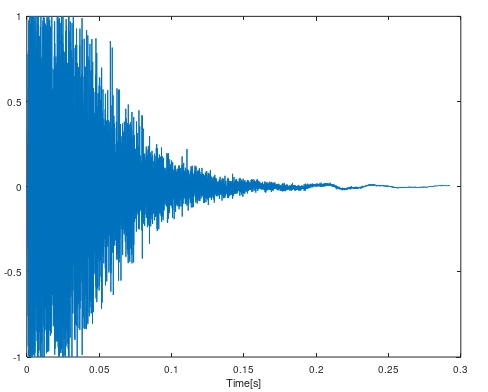
このインパルス応答を使ってFIRフィルタを作ったらどうなるでしょうか。実際に試してみましょう。
GNU Octaveのインストール
信号処理の実験に便利なGNU Octaveというツールがあります。
https://www.gnu.org/software/octave/index
次のサイトなどを参考にインストールしてください。
https://www.kkaneko.jp/tools/win/octave.html
Signalパッケージのインストール
pkg install -forge signal
と入力してSignalパッケージをインストールします。これでディジタル信号処理関係の便利な関数が使用可能になります。インストールにはしばらく時間がかかります。
※最新バージョンの6.2.0だとすでにインストール済みのようです。この手順は必要ありません（エラーになります）
スタートアップファイルの作成
Signalパッケージを起動時に毎回ロードするように、スタートアップファイルを作成します。
起動後何もしていない状態でファイルブラウザに表示されている”現在のディレクトリ”に
.octaverc
というファイルを作成し、以下の記述をして保存してください。なぜかOctaveの内部エディタではこのファイル名で保存させてくれないので、お好みの外部エディタにて作成してください。
pkg load signal
保存したら、Octaveを再起動してください。
スタートアップファイルの作成が面倒であれば起動時に都度上記コマンドを実行するか、これから作成するスクリプトの先頭にこれを入れておく方法でもかまいません。ただしMATLABとは互換性のないコマンドですので、その点に留意してください。
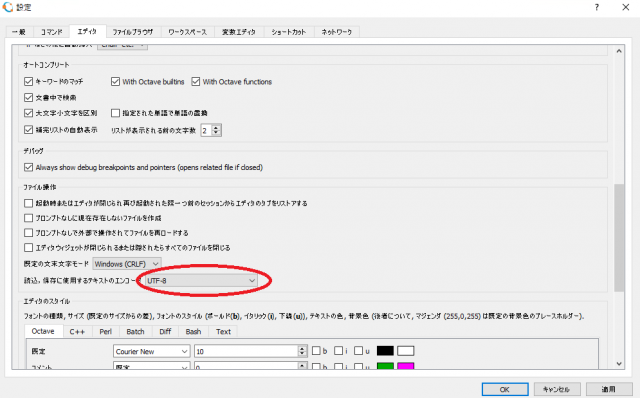
エディタの設定
デフォルト設定のまま日本語のコメント入りのファイルを開くと文字化けするので、エディタの文字コードをUTF-8に変更します。
風呂場のインパルス応答を使ったFIRフィルタ
こちらが風呂場で録音したインパルス応答です。
それにこの猫の鳴き声の音声を入力音声として実験してみます。こちらの素材はVSQ様によって配布されているものです。
こちらのファイルをダウンロード・展開し、bathroom_reverb.mをoctave上のファイルブラウザでダブルクリックするとエディタ上にこのスクリプトが開かれます。
歯車の上に再生マークが乗っているボタンをクリックすると実行できます。
bathroom_reverb.m の内容は下記のとおりです。
[impulse, fs_impulse] = audioread("bathroom_ir.wav"); %インパルス応答ファイルの読み込み
impulse = impulse(:,1); %片chのみ抽出
[audio, fs_audio] = audioread("VSQSE_965_cat_6.wav"); %入力音声の読み込み
audio = audio(:,1); %片chのみ抽出
audio = resample(audio, fs_impulse, fs_audio); %入力音声のサンプリング周波数をインパルス応答のサンプリング周波数に揃える
audio = [audio;zeros(fs_impulse*3,1)]; %入力音声の末尾に3秒の無音を付加
filter_out = filter(impulse, 1, audio); %読み込んだインパルス応答を使って入力音声にFIRフィルタを適用
filter_out = filter_out / max(abs(filter_out)); %最大値が1になるよう正規化
soundsc(filter_out, fs_impulse, 16) %FIRフィルタの出力を音声として再生
audiowrite("cat_bathroom.wav",filter_out, fs_impulse);
impulse_len = length(impulse);
t = (0:(impulse_len-1))/fs_impulse;
plot(t,impulse); %インパルス応答をプロット
xlabel("Time[s]")
figure;
f = (0:1:(impulse_len-1))/impulse_len * fs_impulse;
db = 20*log10( abs( fft( impulse ) ) );
plot( f, db );
xlabel("Frequency[Hz]");
ylabel("Magnitude[dB]");
xlim([0 fs_impulse/2]);
実際にFIRフィルタの処理を行っているのは
filter_out = filter(impulse,1,audio);
の部分で、filterという関数の第1引数にインパルス応答を、第2引数に1を、第3引数に入力の信号を与えます。
こちらが実行結果の音声です。
風呂場のようなエフェクトがかかりました。いわゆるリバーブエフェクトです。風呂場で手を叩いてスマホで録音するだけという簡易な方法でも、案外それらしくなるものです。
このように、FIRフィルタとは入力信号に残響を与えるフィルタと解釈することも出来ます。
リバーブエフェクトに使えるインパルス応答を公開しているサイトが多くあります。
もその一つです。このサイトの中から、”1st Baptist Church Nashville”を試してみようと思います。
Source Sound Category:
Swept sine (logarithmic)
とありますので、手を叩くような雑な方法で測定しているわけではないことがわかります。 Swept-Sine法については次の論文が参考になります。
audioread(“bathroom_ir.wav”);
のファイルを差し替えるだけで動作します。が、かなり演算に時間がかかると思います。
こちらが出力の音声です。教会っぽい感じになりました。
インパルス応答を知っていることで、その振る舞いを再現できるということが体験できるわかりやすい例ではないでしょうか。
FIRフィルタの周波数特性
実際にFIRフィルタを使う場面では、周波数特性が重要な場合が多いでしょう。まず、FIRフィルタの周波数特性の確認方法を考えてみます。
FIRフィルタのインパルス応答がわかっている場合、それをFFTすることで周波数応特性を確認することができます。
実際の操作としては、OctaveなどのツールでFFT関数にインパルス応答を入力するだけです。
風呂場リバーブの周波数特性
ここから先はOctaveを対話的に使っていきます。エディタではなくコマンドウィンドウにコマンド例をコピーアンドペーストしてください。(一回だけbathroom_reverb.mを実行しておいてください)
さきほど試した風呂場リバーブの周波数特性を確認してみます。対象のインパルス応答を格納した変数を
impulse
としたとき、コマンドウィンドウに次のように入力してみます。
plot( abs( fft( impulse ) ) )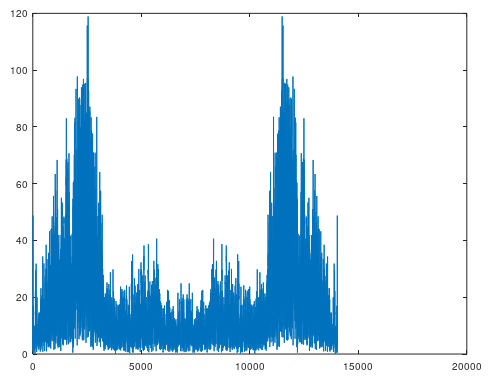
このようなグラフが表示されます。abs()は、複素数の絶対値を取る関数で、振幅応答を知りたいときはこのようにします。
これだと縦軸がリニアスケールですので、dBスケールにしてみます。
plot( 20*log10( abs( fft( impulse ) ) ) )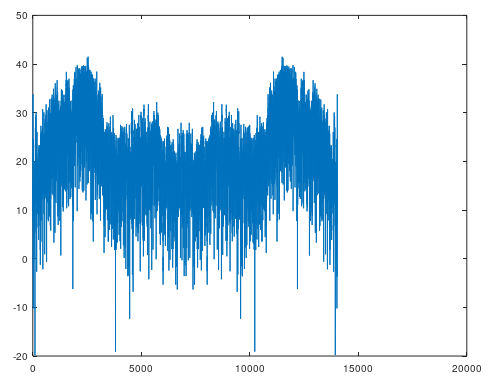
縦軸はdBスケールで読めるようになりましたが、横軸の読み方がよくわかりませんね。
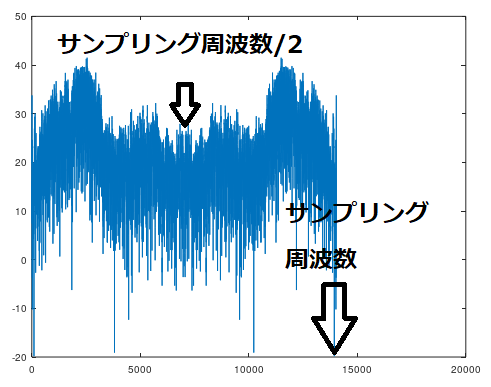
FFTのポイント数をN、サンプリング周波数をfsとすると、プロットの右端がfs*(N-1)/Nとなります。Nが十分大きければ、右端がほぼfsということになります。
サンプリング周波数の1/2以上のところに見えているのは鏡像なので、通常はこれよりも左側に着目します。
次のようにすると周波数を[Hz]で読むことができます。その他、表示範囲を制限するなどして見やすくしています。
f = (0:1:(impulse_len-1))/impulse_len * fs_impulse;
db = 20*log10( abs( fft( impulse ) ) );
plot( f, db );
xlabel("Frequency[Hz]");
ylabel("Magnitude[dB]");
xlim([0 fs_impulse/2]);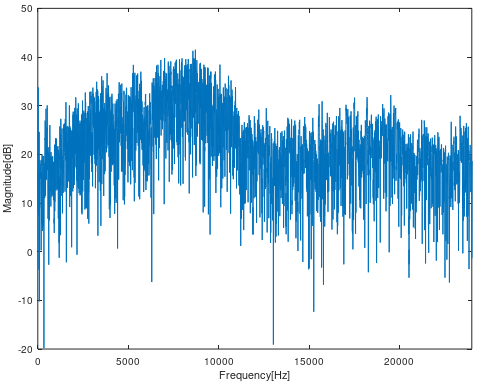
インパルス応答のサンプル数が少ない場合
インパルス応答の説明のところで使ったこちらの場合、周波数特性はどうでしょうか。
impulse = [5.5232e-03 4.7894e-02 1.6184e-01 2.8473e-01 2.8473e-01 1.6184e-01 4.7894e-02 5.5232e-03];
plot( abs( fft( impulse ) ) );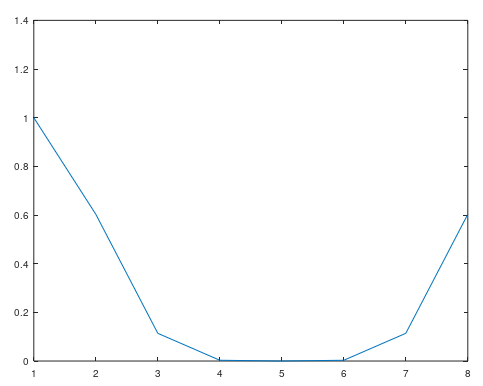
これではよくわかりません。FFTのポイント数が8では少なすぎるのです。fft関数にはポイント数を指定する機能があるので、次のようにしてみます。
plot( abs( fft( impulse, 1000 ) ) );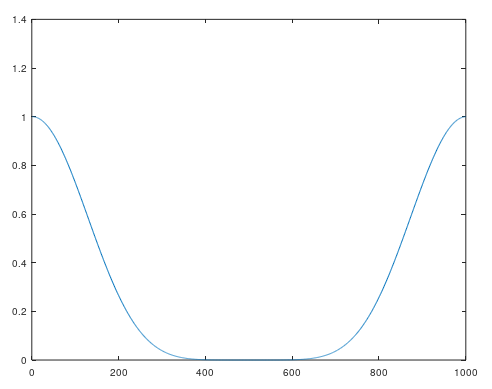
それっぽくなりました。実はローパスフィルタだったことがわかります。
周波数特性を指定してフィルタを設計する
FIRフィルタのインパルス応答をFFTすれば周波数特性が得られるということは、その逆のこと、つまりIFFTを行えば周波数特性からインパルス応答を得ることができ、それをもとにフィルタを設計することができます。
実際に設計する
次の仕様で設計してみたいと思います。
- サンプリング周波数: 48 [kHz]
- タップ数(インパルス応答のサンプル数): 99
- 周波数特性: 数値で指定
周波数特性を定義する
次のような周波数特性にしてみたいと思います。
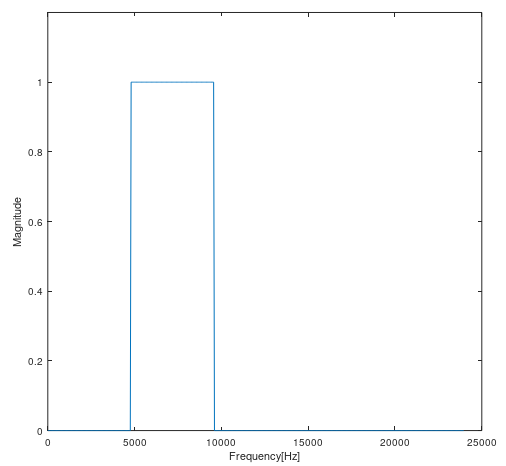
4.8 [kHz]から9.6 [kHz]までを通すバンドパスフィルタです。
IFFTの入力データを作る
0 [Hz]からサンプリング周波数の48 [kHz]までを等分割した周波数特性のデータを作成します。今回は1000分割としました。
f_norm = [zeros(1,100) ones(1,100) zeros(1,300)];サンプリング周波数の1/2までを考えると、このような要領ですね。0が100個続いて、次に1が100個続き、最後は0が300個続きます。
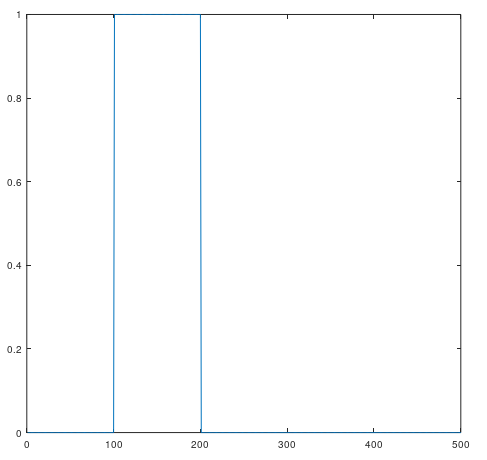
インパルス応答をFFTしたときにはサンプリング周波数の1/2以上のところには鏡像が現れました。これと同じように、上記データに鏡像を付加してやる必要があります。
f_norm = [f_norm fliplr(f_norm(2:end))];fliplrという関数を使ってデータの左右を反転させ、鏡像を作ります。
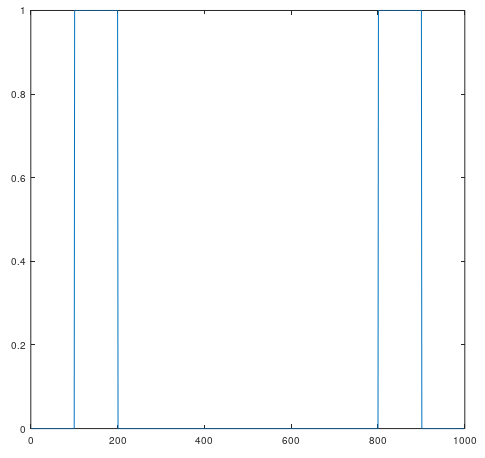
IFFTを行う
これでIFFTを行うデータの準備が整いました。実際にIFFTを行ってみます。real関数は実数のみを取り出す関数です。今回虚数部は0になるはずですが、念の為入れます。
ifft_out = real(ifft(f_norm));
stem(ifft_out);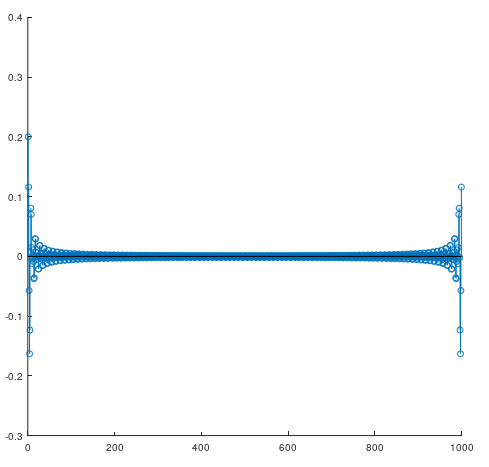
このようなインパルス応答が得られました。
インパルス応答を切り出す
今回、フィルタのタップ数が99ですから、ここから99サンプル分を切り出します。切り出す場所ですが、左端から99個ではなく、次の図に示す99個になります。IFFTやFFTの結果をグラフ表示したとき、右端と左端はつながっていると考えてください。
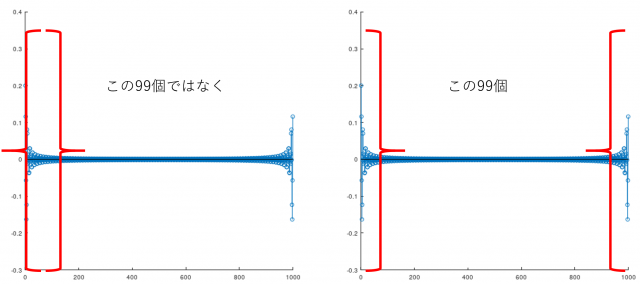
タップ数として奇数を選んでいる理由は位相特性の面で偶対称または奇対称なインパルス応答とした方が好ましいためです。偶数タップ数の場合、0.5サンプルのシフトが必要なため、IFFTの長さを倍にして計算するなどやや面倒な手順が必要になります。位相特性を気にしない場合、対称性は厳密に考えなくても問題ありません。
fftshiftという便利な関数が用意されています。これを使うと簡単になりそうです。
stem( fftshift( ifft_out ) )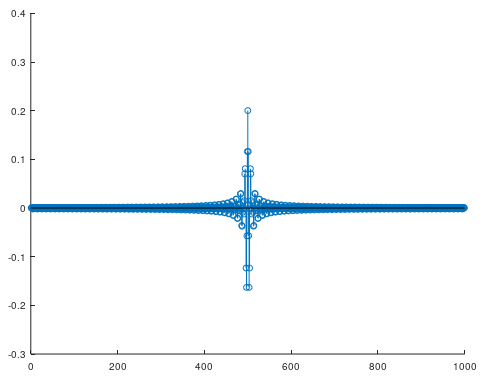
このような関数が用意されていることからも、FFTやIFFTの結果というのは右端と左端がつながっていることが実感できると思います。印刷して丸めるた方が現実に近いのです。
ここから、中心の99サンプルを切り出せばよいわけです。
taps = 99;
ifft_shift = fftshift(ifft_out);
center = ceil(length(f_norm)/2);
impulse_rect = ifft_shift((center-floor(taps/2):(center+floor(taps/2))))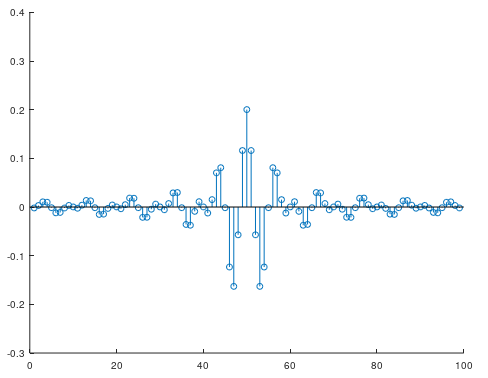
このようにしてインパルス応答を切り出すことができました。
周波数特性を確認する
この切り出したインパルス応答の周波数特性を確認してみます。
plot( abs( fft( impulse_rect, 1000 ) ) );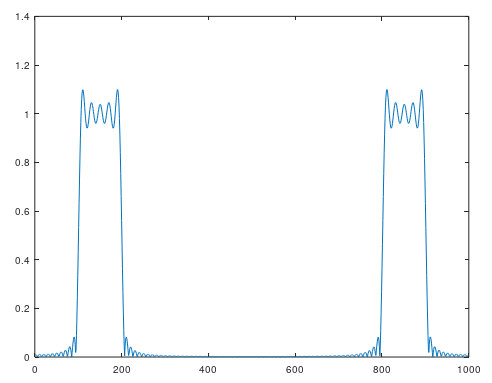
なんだかギザギザしていますね。dBスケールで見てみましょう。
plot( 20*log10( abs( fft( impulse_rect, 1000 ) ) ) );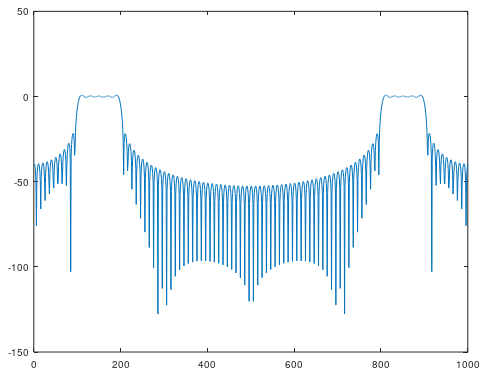
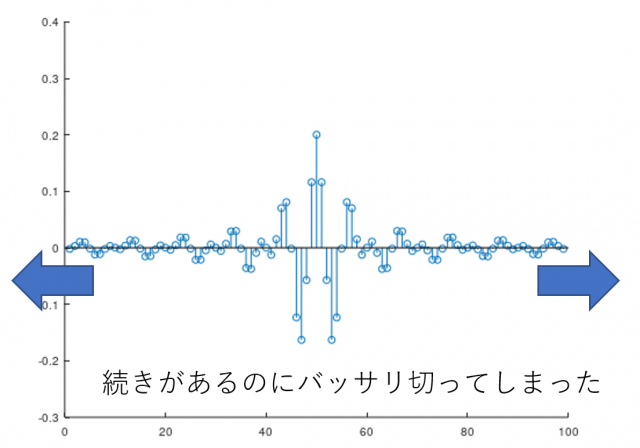
あまりきれいな特性ではないですね。これには原因があって、インパルス応答を99サンプル分切り出しましたが実際にはその両端にも応答が続きます。それをバッサリ切ってしまったために、このようなことが起こります。
窓関数をかける
インパルス応答をバッサリ切ってしまったために周波数特性がギザギザする現象をギブス現象と呼びます。これを軽減するために窓関数というものを利用する方法が知られています。
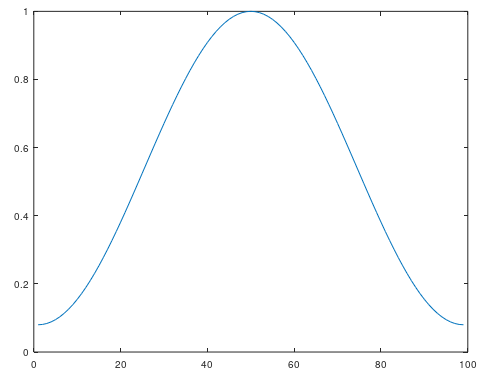
これはハミング窓と呼ばれる窓関数です。これを切り出したインパルス応答に掛け算することで、一番大切な中央付近の情報はなるべく保持しつつ、バッサリ切った両端部分は減衰させその影響を軽減します。
Octaveでは、ベクトルの成分同士の掛け算(アダマール積)を行う演算子は .* です。
w = hamming(taps)';
impulse_hamming = impulse_rect.*w;
stem(impulse_hamming);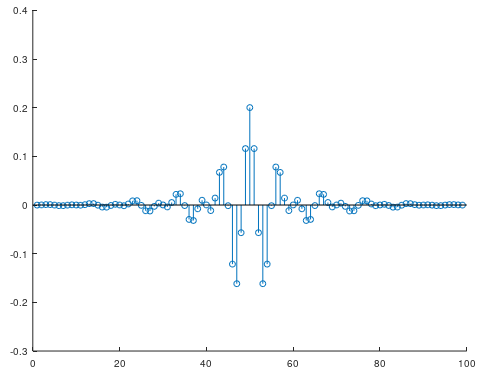
両端部分の不連続な感じが軽減されました。周波数特性を見てみましょう。
plot( 20*log10( abs( fft( impulse_hamming, 1000 ) ) ) );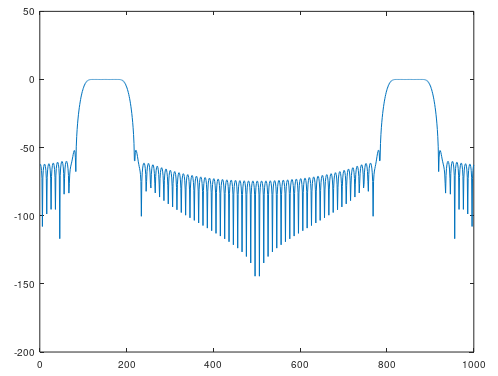
だいぶマシになりました。グラフ表示を整えてみます。
周波数特性の最終確認
fs = 48e3;
fft_n = 1000;
f = (0:1:(fft_n-1))/fft_n * fs;
fft_out = fft( impulse_hamming, 1000 );
mag = abs(fft_out);
phase = unwrap(angle(fft_out));
plot( f,20*log10( mag ) );
xlabel("Frequency[Hz]");
ylabel("Magnitude[dB]");
xlim([0 fs/2]);
ylim([-100 10]);
figure;
plot( f,phase );
xlabel("Frequency[Hz]");
ylabel("Phase[rad]");
xlim([0 fs/2]);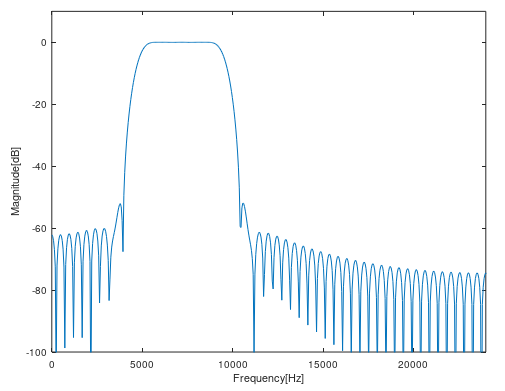
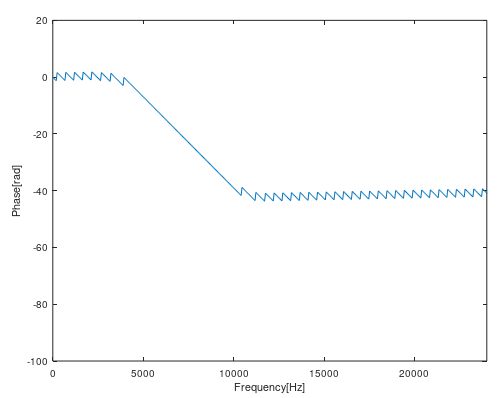
今度は位相特性もプロットしてみました。angle関数とunwrap関数を使うことで簡単に位相特性を知ることができます。
音声への適用
このフィルタを猫の鳴き声に適用してみます。
[audio, fs_audio] = audioread("VSQSE_965_cat_6.wav");
audio = audio(:,1);
audio = resample(audio, fs, fs_audio);
filter_out = filter(impulse_hamming, 1, audio);
soundsc(filter_out, fs_impulse, 16)
audiowrite("cat_bpf.wav",filter_out, fs_impulse);スクリプト全体
ここまでで使ったスクリプトの全体を示します。
fs = 48e3;
taps = 99;
f_norm = [zeros(1,100) ones(1,100) zeros(1,300)]; %周波数特性を定義
%f_norm = [ones(1,50)*0.1 ones(1,50)*0.01, ones(1,50) ones(1,50)*0.5 zeros(1,300)];
f_norm = [f_norm fliplr(f_norm(2:end))]; %鏡像の付加
ifft_out = real(ifft(f_norm)); %IFFT
ifft_shift = fftshift(ifft_out); %切り出したい位置を中心に移動
center = ceil(length(f_norm)/2);
impulse_rect = ifft_shift((center-floor(taps/2):(center+floor(taps/2)))) %インパルス応答の切り出し
w = hamming(taps)'; %窓関数
impulse_hamming = impulse_rect.*w; %窓関数を適用
stem(impulse_hamming); %以下グラフ表示操作
fft_n = 1000;
f = (0:1:(fft_n-1))/fft_n * fs;
fft_out = fft( impulse_hamming, 1000 );
mag = abs(fft_out);
phase = unwrap(angle(fft_out));
figure;
plot( f,20*log10( mag ) );
xlabel("Frequency[Hz]");
ylabel("Magnitude[dB]");
xlim([0 fs/2]);
ylim([-100 10]);
figure;
plot( f,phase );
xlabel("Frequency[Hz]");
ylabel("Phase[rad]");
xlim([0 fs/2]);
[audio, fs_audio] = audioread("VSQSE_965_cat_6.wav"); %以下音声出力
audio = audio(:,1);
audio = resample(audio, fs, fs_audio);
filter_out = filter(impulse_hamming, 1, audio);
soundsc(filter_out, fs_impulse, 16)
audiowrite("cat_bpf.wav",filter_out, fs_impulse);この中で、
f_norm = [zeros(1,100) ones(1,100) zeros(1,300)];の部分を色々と変えることで様々な特性のフィルタを設計することができます。たとえば、
f_norm = [ones(1,50)*0.1 ones(1,50)*0.01, ones(1,50) ones(1,50)*0.5 zeros(1,300)];としてみます。
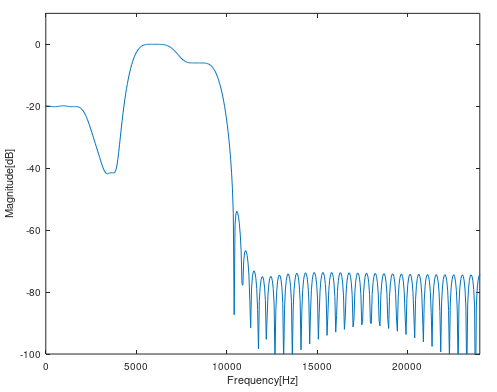
このような変わった特性のフィルタも作ることが可能です。
偶数タップ数にも対応したバージョン
詳しい説明は省きますが、IFFTの長さを倍にしてから結果を間引くことで0.5サンプルのシフトを行い、偶数タップ数に対応したスクリプトになります。
fs = 48e3;
taps = 100;
f_norm = [zeros(1,100) ones(1,100) zeros(1,300)];
%f_norm = [ones(1,50)*0.1 ones(1,50)*0.01, ones(1,50) ones(1,50)*0.5 zeros(1,300)];
f_norm = [f_norm*2 zeros(1,length(f_norm))];
f_norm = [f_norm fliplr(f_norm(2:end))];
ifft_out = real(ifft(f_norm));
ifft_shift = downsample(fftshift(ifft_out),2,mod(taps,2));
center = ceil(length(ifft_shift)/2);
impulse_rect = [ifft_shift( (center-ceil(taps/2)+1):(center+floor(taps/2)))];
w = hamming(taps)';
impulse_hamming = impulse_rect.*w;
stem(impulse_hamming);
fft_n = 1000;
f = (0:1:(fft_n-1))/fft_n * fs;
fft_out = fft( impulse_hamming, 1000 );
mag = abs(fft_out);
phase = unwrap(angle(fft_out));
plot( f,20*log10( mag ) );
xlabel("Frequency[Hz]");
ylabel("Magnitude[dB]");
xlim([0 fs/2]);
ylim([-100 10]);
figure;
plot( f,phase );
xlabel("Frequency[Hz]");
ylabel("Phase[rad]");
xlim([0 fs/2]);以上のような設計方法を窓関数法と呼びます。今回はOctaveでスクリプトを作成して設計してみましたが、こういった手順を自動化できるツールが多くありますので実際にはそれを利用することが多いです。例えば、次のWebサイトなどがあります。
石川高専 山田洋士 研究室ホームページ Digital Filter Design Services
上記スクリプトはこちらからダウンロードできます。
おわりに
ほとんど数式を登場させずにFIRフィルタを解説してみました。まずはこのように直感的解釈や実験を通してその動きを肌で感じることが大切だと考えています。次回は、IIRフィルタについて解説してみたいと思います。
参考文献
Cerevoからのお知らせ
現在Cerevoでは各種エンジニアの採用、またハードウェア共同開発・受託開発を絶賛募集しております。それぞれご関心お持ちいただける方は、以下の専用お問い合わせフォームよりご連絡お待ちしております。
- 現在募集している職種
https://cerevo.com/recruit/
- ハードウェア共同開発および受託開発のご相談
https://cerevo.com/contact/sales/
著者プロフィール
- Cerevo 電気エンジニア
最近の投稿
05. 実験・比較2021.12.10中華ログペリアンテナを120%活かした社内EMC試験の方法 – アンテナファクタ付で販売も
資格試験2021.08.10第一級陸上無線技術士試験を受験した電気エンジニアの勉強法
02. ソフトウェア2021.05.23ハードウェア量産において避けられないEMC試験に落ちないための心がけ
05. 実験・比較2021.05.15呼気中アルコール濃度変化をアルコール検知器とインパルス応答で見る
