とにかくラフに設計するディジタルフィルタ

はじめに

以前に
数式をほとんど使わずに理解するディジタルフィルタ
アナログ視点で理解するディジタルフィルタ。FIRフィルタとIIRフィルタの構造とは
という記事を執筆し、ご好評をいただきました。
実務上はフィルタの設計ツールを使うことが多いかと思います。しかし、必要なパラメータが多すぎて何を入力すればよいかわからない、もしくは細かいことは気にしないのでとにかく早く設計したいこともあるでしょう。

窓関数法

FIRフィルタのタップ係数を算出するのにとてもシンプルな方法が窓関数法として知られています。これは直接的に周波数特性を指定して設計する方法です。前述の過去記事にて細かい部分は説明していますので、実装だけを示します。

実際のコード

過去記事にてMATLAB or Octaveのスクリプトとして紹介したものをPythonに移植したものです。

f_normにナイキスト周波数までのゲインを等間隔で代入します。刻み幅は任意です。同時に、タップ数とサンプリング周波数も指定します。

最後に、実際に出来上がったフィルタの周波数特性が表示されます。

impulse_hammingが実際のタップ係数になります。

import numpy as np
from matplotlib import pyplot as plt

#サンプリング周波数とタップ数の指定
fs = 48e3
taps = 100

#周波数特性を定義
f_norm = np.concatenate([0.01*np.ones(50), 1.0*np.ones(100), 1.0 + 0.2*np.sin(np.arange(0, np.pi*10, 0.025)), 0.5*np.zeros(200)])

#2倍にアップサンプル(偶数タップ数対応)
f_norm = np.concatenate([f_norm*2, np.zeros((f_norm.shape[0]))])

#鏡像の付加
f_norm = np.concatenate( [f_norm, f_norm[-1:0:-1]])

#IFFTで時間領域に変換し、整列
ifft_out = np.real(np.fft.ifft(f_norm))
ifft_shift = np.fft.fftshift(ifft_out)

#1/2にダウンサンプル
ifft_shift = ifft_shift[::2]

#矩形窓の切り出し
center = np.floor( ifft_shift.shape[0]/2)
start_point = int((center-np.ceil(taps/2)))
end_point = int(center+np.floor(taps/2))
impulse_rect = ifft_shift[start_point:end_point]

#窓関数処理
w = np.hamming(taps)
impulse_hamming = impulse_rect*w

#周波数特性の表示
freqs = np.fft.fftfreq(1024, 1/fs)
plt.plot(freqs[0:511],abs(np.fft.fft(impulse_hamming,1024))[0:511])
plt.show()

設計したフィルタの周波数特性

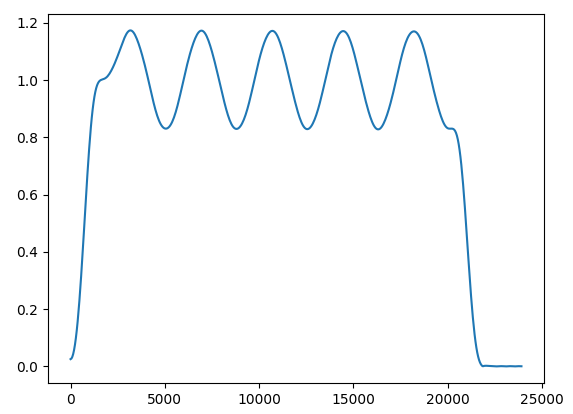
このような複雑な周波数特性も簡単に得られます。

おわりに

驚くほど簡単なコードですが実際に紹介されている例をあまり見ないので記事にしてみました。信号処理などの参考になれば幸いです。